浙教版八年级上册数学单元测试 第1章三角形的初步认识（含解析）

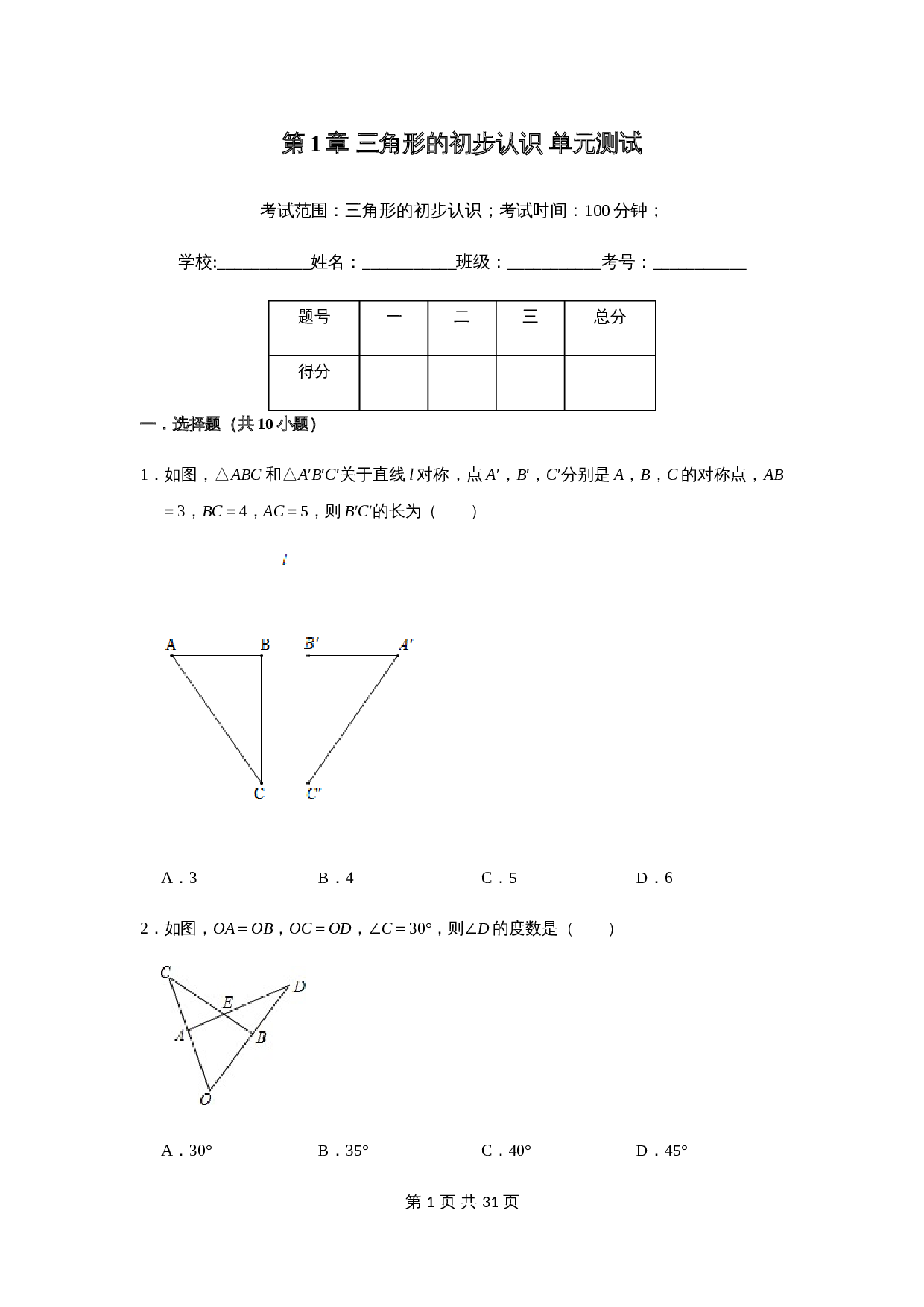
第 1 章 三角形的初步认识 单元 测试 考试范围：三角形的初步认识；考试时间： 100 分钟； 学校 :___________ 姓名： ___________ 班级： ___________ 考号： ___________ 题号 一 二 三 总分 得分 一 ．选择题（共 10 小题） 1 ．如图，△ ABC 和△ A ′ B ′ C ′关于直线 l 对称，点 A ′， B ′， C ′分别是 A ， B ， C 的对称点， AB ＝ 3 ， BC ＝ 4 ， AC ＝ 5 ，则 B ′ C ′的长为（　　） A ． 3 B ． 4 C ． 5 D ． 6 2 ．如图， OA ＝ OB ， OC ＝ OD ，∠ C ＝ 30 °，则∠ D 的度数是（　　） A ． 30 ° B ． 35 ° C ． 40 ° D ． 45 ° 3 ．下列△ ABC 与△ DEF 不一定全等的是（　　） A ．∠ A ＝∠ D ， BC ＝ EF ，∠ B ＝∠ E B ．∠ A ＝∠ D ，∠ B ＝∠ E ， AB ＝ DE C ．∠ A ＝∠ D ， AB ＝ DE ， BC ＝ EF D ．∠ C ＝∠ F ＝ 90 °， AB ＝ DE ， AC ＝ DF 4 ．下列语句中，是定义的是（　　） A ．两点确定一条直线 B ．在同一平面内，不相交的两条直线叫做平行线 C ．三角形的角平分线是一条线段 D ．同角的余角相等 5 ．如图，在△ ABC 中，∠ 1 ＝∠ 2 ＝∠ 3 ＝∠ 4 ．则下列说法中，正确的是（　　） A ． AD 是△ ABE 的中线 B ． AE 是△ ABC 的角平分线 C ． AF 是△ ACE 的高线 D ． AE 是△ ABC 的中线 6 ．如图，△ ACB ≌△ A ′ CB ′，∠ BCB ′＝ 25 °，则∠ ACA ′的度数为（　　） A ． 35 ° B ． 30 ° C ． 25 ° D ． 20 ° 7 ．下列每组数分别是三根小木棒的长度，用它们能摆成三角形的是（　　） A ． 3 cm ， 4 cm ， 8 cm B ． 8 cm ， 7 cm ， 15 cm C ． 5 cm ， 5 cm ， 11 cm D ． 13 cm ， 14 cm ， 20 cm 8 ．下列各命题中假命题的是（　　） A ．全等三角形的对应角相等 B ．如果两个数相等，那么它们的绝对值相等 C ．两直线平行，同位角相等 D ．如果两个角相等，那么这两个角是对顶角 9 ．在△ ABC 中，∠ B 、∠ C 的平分线交于点 O ，若∠ BOC ＝ 132 °，则∠ A 的度数为（　　） A ． 42 ° B ． 48 ° C ． 84 ° D ． 100 ° 10 ．在△ ABC 中， 2 （∠ A + ∠ B ）＝ 3 ∠ C ，则∠ C 的补角等于（　　） A ． 36 ° B ． 72 ° C ． 108 ° D ． 144 ° 二．填空题（共 6 小题） 11 ．如图所示，点 D ， E ， F 分别是△ ABC 的边 BC ， AC ， AB 上的点，则∠ 1 ，∠ 2 ，∠ 3 ，∠ 4 ，∠ 5 ，∠ 6 这六个角的度数的和是 　 　 ． 12 ．已知三角形的三个内角的比为 2 ： 3 ： 5 ，则最大角的大小为 　 　 ． 13 ．如图， AD 为△ ABC 的中线， BE 为△ ABD 的中线，若△ ABC 的面积为 40 ，且 DE ＝ 4 ，则点 C 到直线 AD 的距离为 　 　 ． 14 ．如图，已知 AC ＝ BD ，要使得△ ABC ≌△ DCB ，根据“ SSS ”判定方法，需要再添加的一个条件是 　 　 ． 15 ．如图所示的折线图形中， α + β ＝ 　 　 ． 16 ．已知在△ ABC 中，∠ A ＝ 30 °， BD 是△ ABC 的高，∠ BCD ＝ 80 °，则∠ ACB ＝ 　 　 °． 三．解答题（共 7 小题） 17 ．如图，在△ ABC 中，∠ A ＝∠ DBC ＝ 36 °，∠ C ＝ 72 °．求∠ 1 ，∠ 2 的度数． 18 ．如图， A ， B 分别是线段 OC ， OD 上的点， OC ＝ OD ， OA ＝ OB ．求证：△ OAD ≌△ OBC ． 19 ．如图，在△ ABC 和△ DCB 中， AB ⊥ AC ， CD ⊥ BD ， AB ＝ DC ， AC 与 BD 交于点 O ．求证： AC ＝ BD ． 20 ．如图， A ， D ， E 三点在同一直线上，且△ BAD ≌△ ACE ． （ 1 ）求证： BD ＝ DE + CE ； （ 2 ）请你猜想△ ABD 满足什么条件时， BD ∥ CE ． 21 ．如图， AC 是∠ BAE 的平分线，点 D 是线段 AC 上的一点，∠ C ＝∠ E ， AB ＝ AD ． 求证：△ BAC ≌△ DAE ． 22 ．小亮在学习中遇到这样一个问题： 如图 1 ，在△ ABC 中，∠ C ＞∠ B ， AE 平分∠ BAC ， AD ⊥ BC 于 D ． 猜想∠ B 、∠ C 、∠ EAD 的数量关系，说明理由． （ 1 ）小亮阅读题目后，没有发现数量关系与解题思路．于是尝试带入∠ B 、∠ C 的值求 ∠ EAD 值，得到下面几组对应值： ∠ B / 度 10 30 30 20 20 ∠ C / 度 70 70 60 60 80 ∠ EAD / 度 30 20 15 a 30 上表中 a ＝ 　 　 ． （ 2 ）猜想∠ B 、∠ C 、∠ EAD 的数量关系，说明理由． （ 3 ）小亮突发奇想，交换 B 、 C 两个字母位置，如图 2 ，过 EA 的延长线是一点 F 作 FD ⊥ BC 交 CB 的延长线于 D ，当∠ B ＝ 80 °、∠ C ＝ 20 °时，∠ F 度数为 　 　 °． 23 ． Rt △ ABC 中，∠ C ＝ 90 °，点 D 、 E 分别是△ ABC 边 AC 、 BC 上的点，点 P 是一动点．令∠ PDA ＝∠ 1 ，∠ PEB ＝∠ 2 ，∠ DPE ＝∠ α ． （ 1 ）若点 P 在线段 AB 上，如图（ 1 ）所示，且∠ α ＝ 30 °，则∠ 1+ ∠ 2 ＝ 　 　 °； （ 2 ）若点 P 在 AB 上运动，如图（ 2 ）所示，则∠ α 、∠ 1 、∠ 2 之间有何关系？猜想并说明理由． （ 3 ）若点 P 运动到边 AB 的延长线上，如图（ 3 ）所示，则∠ α 、∠ 1 、∠ 2 之间有何关系？ 猜想并说明理由． （ 4 ）若点 P 运动到△ ABC 形外，如图（ 4 ）所示，则∠ α 、∠ 1 、∠ 2 的关系为： 　 　 ． 第 1 章 三角形的初步