【基础提升】沪科版八年级上册数学 第14章全等三角形 单元测试（B卷·提升卷）（含答案）

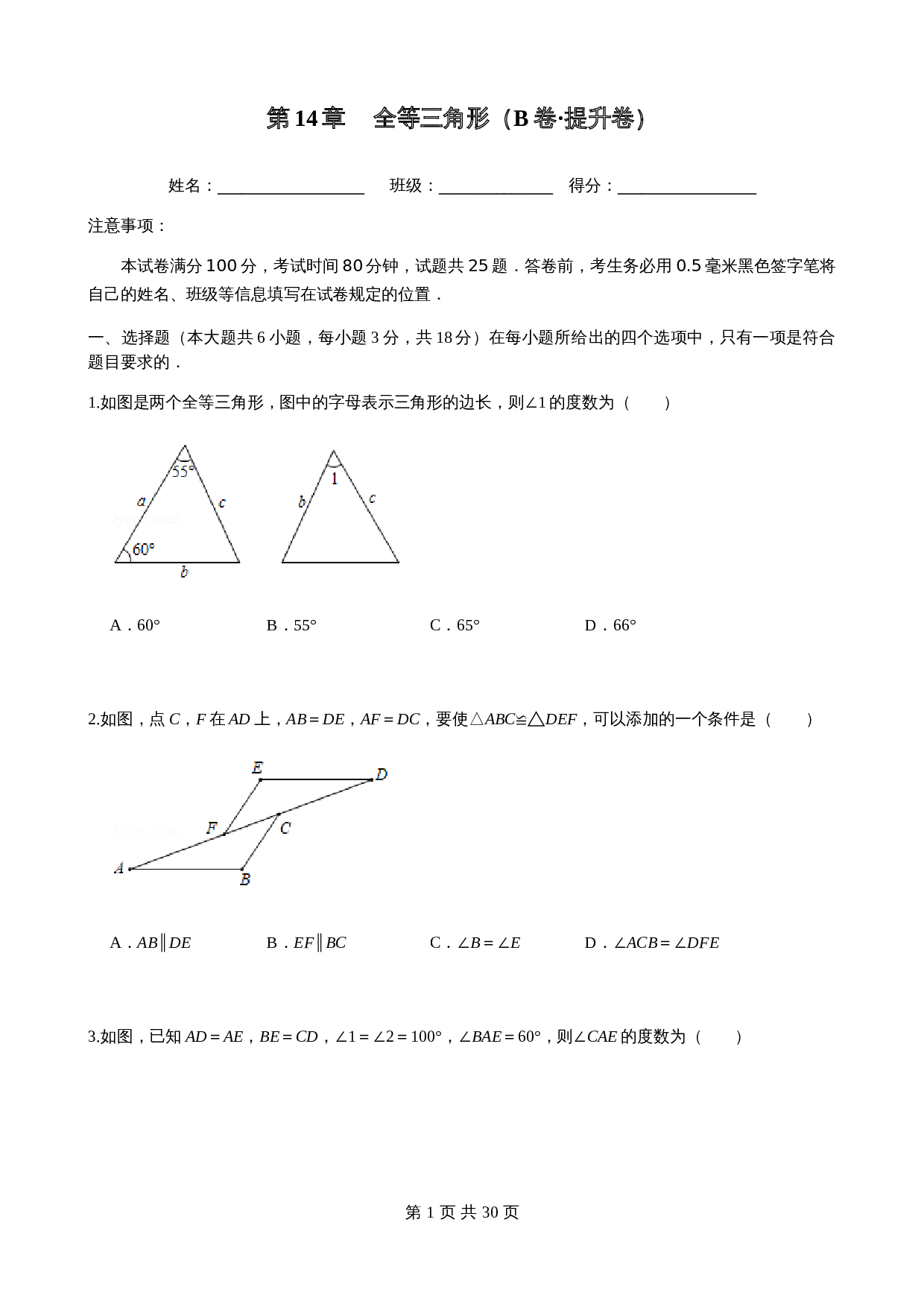
第 1 4 章 全等三角形 （B卷·提升卷） 姓名 ：_ _________________ 班级 ：_ _____________ 得分 ：_ ________________ 注意事项： 本试卷满分1 0 0分，考试时间 80 分钟，试题共2 5题 ． 答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置 ． 一、选择题（本大题共 6 小题，每小题 3 分，共 18 分） 在每小题所给出的四个选项中，只有一项是符合题目要求的． 1. 如图是两个全等三角形，图中的字母表示三角形的边长，则∠ 1 的度数为（　　） A ． 60 ° B ． 55 ° C ． 65 ° D ． 66 ° 2. 如图，点 C ， F 在 AD 上， AB ＝ DE ， AF ＝ DC ，要使△ ABC ≌△ DEF ，可以添加的一个条件是（　　） A ． AB ∥ DE B ． EF ∥ BC C ．∠ B ＝∠ E D ．∠ ACB ＝∠ DFE 3. 如图，已知 AD ＝ AE ， BE ＝ CD ，∠ 1 ＝∠ 2 ＝ 100 °，∠ BAE ＝ 60 °，则∠ CAE 的度数为（　　） A ． 20 ° B ． 30 ° C ． 40 ° D ． 50 ° 4. 如图，点 B 、 C 分别在线段 NM 、 NA 上，在△ ABC 中，∠ A ：∠ ABC ：∠ BCA ＝ 3 ： 5 ： 10 ，且△ ABC ≌△ MNC ，则∠ BCM ：∠ NBA 等于（　　） A ． 1 ： 2 B ． 1 ： 3 C ． 1 ： 4 D ． 1 ： 5 5. 下列说法中，正确说法的个数有（　　） ① 角是轴对称图形，对称轴是角的平分线； ② 等腰三角形至少有 1 条对称轴，至多有 3 条对称轴； ③ 关于某直线对称的两个三角形一定是全等三角形； ④ 一个锐角和一条边相等的两个三角形全等 A ． 1 个 B ． 2 个 C ． 3 个 D ． 4 个 6. 如图，矩形 ABCD 中， BC ＝ 2 AB ，对角线相交与 O 点，过 C 点作 CE ⊥ BD 交 BD 于 E 点， H 为 BC 中点，连接 AH 交 BD 于 G 点，交 EC 的延长线于 F 点，下列 4 个结论： ① EH ＝ AB ； ② ∠ ABG ＝∠ HEC ； ③ △ ABG ≌△ HEC ； ④ CF ＝ BD ．正确的结论是（　　） A ． ①②④ B ． ①④ C ． ③④ D ． ①③④ 二、填空题（本大题共 12 小题，每小题 3 分，共 36 分．不需写出解答过程，请把答案直接填写在横线上） 7. 已知△ ABC ≌△ A ′ B ′ C ′， AB ＝ 6 ， BC ＝ 7 ， CA ＝ 8 ，则△ A ′ B ′ C ′的周长是 　　　 ． 8. 若△ ABC ≌△ A 1 B 1 C 1 ， A 、 B 的对应点分别为 A 1 、 B 1 ，∠ A ＝ 110 °，∠ B ＝ 40 °，则∠ C 1 ＝ 　　　　 ． 9. 如图，△ ABC ≌△ DEF ， BE ＝ 3 ， AE ＝ 2 ，则 DE 的长是 　　 ． 10. 在△ ABC 和△ DEF 中，给出下列四组条件： ① ∠ B ＝∠ E ， BC ＝ EF ，∠ C ＝∠ F ； ② AB ＝ DE ，∠ B ＝∠ E ， BC ＝ EF ； ③ AB ＝ DE ， BC ＝ EF ， AC ＝ DF ： ④ AB ＝ DE ， AC ＝ DF ，∠ B ＝∠ E 能使△ ABC ≌△ DEF 的条件是 　 　　　 　 （写出所有正确的序号） 11. 如图，在△ ABC 中， AD ⊥ BC ， BE ⊥ AC ，垂足分别为点 D 、 E ， AD 与 BE 交于点 F ， BF ＝ AC ，∠ ABE ＝ 22 °，则∠ CAD 的度数是 　　　　 ． 12. 如图，△ ACE ≌△ DBF ，如果∠ E ＝∠ F ， DA ＝ 10 ， CB ＝ 2 ，那么线段 AB 的长是 　　 ． 13. 如图所示，△ ABC ≌△ ADE ，且∠ DAE ＝ 55 °，∠ B ＝ 25 °，则∠ ACG ＝ 　　　　 ． 14. 如图，△ ABE ≌△ ACD ，∠ A ＝ 60 °，∠ B ＝ 25 °，则∠ DOE 的度数为 　　　　 ． 15. 如图，在四边形 ABCD 中， AC 平分∠ BAD ， BC ＝ CD ＝ 2 ， AB ＝ 5 ， AD ＝ 3 ，则 AC 的长为 　　　　　　 ． 16. 如图，△ ABC 和△ BDE 都是等边三角形，且点 E 在 AD 边上，已知∠ ECB ＝ 35 °．则∠ ABE ＝ 　　　　 ． 17. 如图，△ ABC 中， D ， E 分别是边 AB ， AC 上的点， DE 的延长线交过 C 点的 AB 的平行线于点 F ．若 DE ＝ FE ， AB ＝ 5 ， CF ＝ 3 ，则 BD 的长是 　　 ． 18. 如图，在等腰直角三角形 ABC 中，∠ ACB ＝ 90 °， AC ＝ BC ＝ 4 ， D 为 BC 中点， E 为 AC 边上一动点，连接 DE ，以 DE 为边并在 DE 的右侧作等边△ DEF ，连接 BF ，则 BF 的最小值为 　　 ． 三、解答题（本大题共 7 小题，共 44 分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤） 19. 如图， F 是等边△ ABC 的边 AC 的中点， D 在边 BC 上，△ DEF 是等边三角形，连接 CE ， ED 的延长线交 AB 于 H ，求证： CF + CE ＝ CD ． 20. 如图，在△ ABC 中，点 D 、 E 分别在 AB 、 AC 上， AB ＝ AC ， BD ＝ CE ， BE 与 CD 交于 O ．求证：∠ ABE ＝∠ ACD ． 21. 已知：如图，菱形 ABCD 中，点 E ， F 分别在 AB ， AD 边上， AE ＝ AF ，连接 CE ， CF ．求证：∠ AEC ＝∠ AFC ． 22. 如图，∠ BAD ＝∠ CAE ＝ 90 °， AB ＝ AD ， AE ＝ AC ，点 D 在线段 CE 上，点 B 在线段 CF 上， AF ⊥ CF ． （ 1 ）若 AC ＝ 10 ，求四边形 ABCD 的面积； （ 2 ）求证： CE + BF ＝ CD ． 23. 如图在四边形 ABCD 中， AD ∥ BC ， AD ＝ 5 cm ， BC ＝ 9 cm ． M 是 CD 的中点 P 是 BC 边上的一动点 P 与 B ， C 不重合），连接 PM 并延长交 AD 的延长线于 Q ． （ 1 ）试说明不管点 P 在何位置，四边形 PCQ