苏科版七年级数学下册单元测试 第12章 证明（提高篇）【提优专练】（含答案）

第 12 章 证明（提高篇） 一、单选题 （本大题共 1 0 小题， 每小题3分， 共 3 0 分） 1 ．下列语句中，不属于命题的是（     ）． A ．两直线平行，内错角相等 B ．三角形的内角和是不是等于 180° C ．同位角相等 D ．三角形的一个外角大于任何一个与它不相邻的内角 2 ．下列命题中，属于假命题的是（　　） A ．直角三角形两 锐角互余 B ． 两个互余的 角不相等 C ．在同一平面内垂直于同一条直线的两直线平行 D ．对顶角相等 3 ．下列命题都是真命题，其中逆命题也正确的是（      ） A ．若 ，则 B ．若 ，则 C ．若 ，则 D ．若 ，则 4 ．下列命题： ① 如果 a ＞ b ，那么 a+c ＞ b+c ； ② 如果 a≥0 ， b ＜ 0 ，那么 ab≤0 ； ③ 直角三角形有两个锐角 . 其中原命题与其逆命题都是真命题的有（     ） A ． 1 个 B ． 2 个 C ． 3 个 D ． 0 个 5 ．下列结论中错误的有（　　） ① 三角形至多有两条高在三角形的外部； ② 一个多边形的边数每增加一条，这个多边形的内角和就增加 ； ③ 两条直线被第三条直线所截，则同旁内角一定互补； ④ 在图形的平移中，连接对应点的线段互相平行且相等； ⑤ 在 中，若 ，则 为直角三角形． A ． 1 个 B ． 2 个 C ． 3 个 D ． 4 个 6 ．说明 “ 若 ，则 ” 是假命题的反例可以是（      ） A ． ， B ． ， C ． ， D ． ， 7 ．下列命题： ① 对顶角相等； ② 同位角相等，两直线平行； ③ 若 ，则 ； ④ 若 ，则 它们的逆命题一定成立的有（      ） A ． ①②③④ B ． ①④ C ． ②④ D ． ② 8 ．若 ，则下列不等式中正确的是（      ） A ． B ． C ． D ． 9 ．下列语句： ① 在同一平面内，若三条直线只有两个交点，则其中两条直线互相平行； ② 如果两条平行线被第三条所截，同旁内角相等，那么这两条平行线都与第三条直线垂直； ③ 过一点有且只有一条直线与已知直线平行，其中（　　） A ． ①② 是真命题 B ． ②③ 是真命题 C ． ①③ 是真命题 D ．以上结论皆是假命题 10 ．试说明 “ 若 ， ， ，则 ” 是真命题．以下是排乱的推理过程： ① 因为 （已知）； ② 因为 ， （已知）； ③ 所以 ， （等式的性质）； ④ 所以 （等量代换）； ⑤ 所以 （等量代换）． 正确的顺序是 (     ) A ． ①→③→②→⑤→④ B ． ②→③→⑤→①→④ C ． ②→③→①→⑤→④ D ． ②→⑤→①→③→④ 填空题 （本大题共 8 小题， 每小题4分， 共 32 分） 11 ．下列语句中，命题有 _______ 个 ． ① 对顶角相等； ② 内错角相等； ③∠1 ＞ ∠2 吗？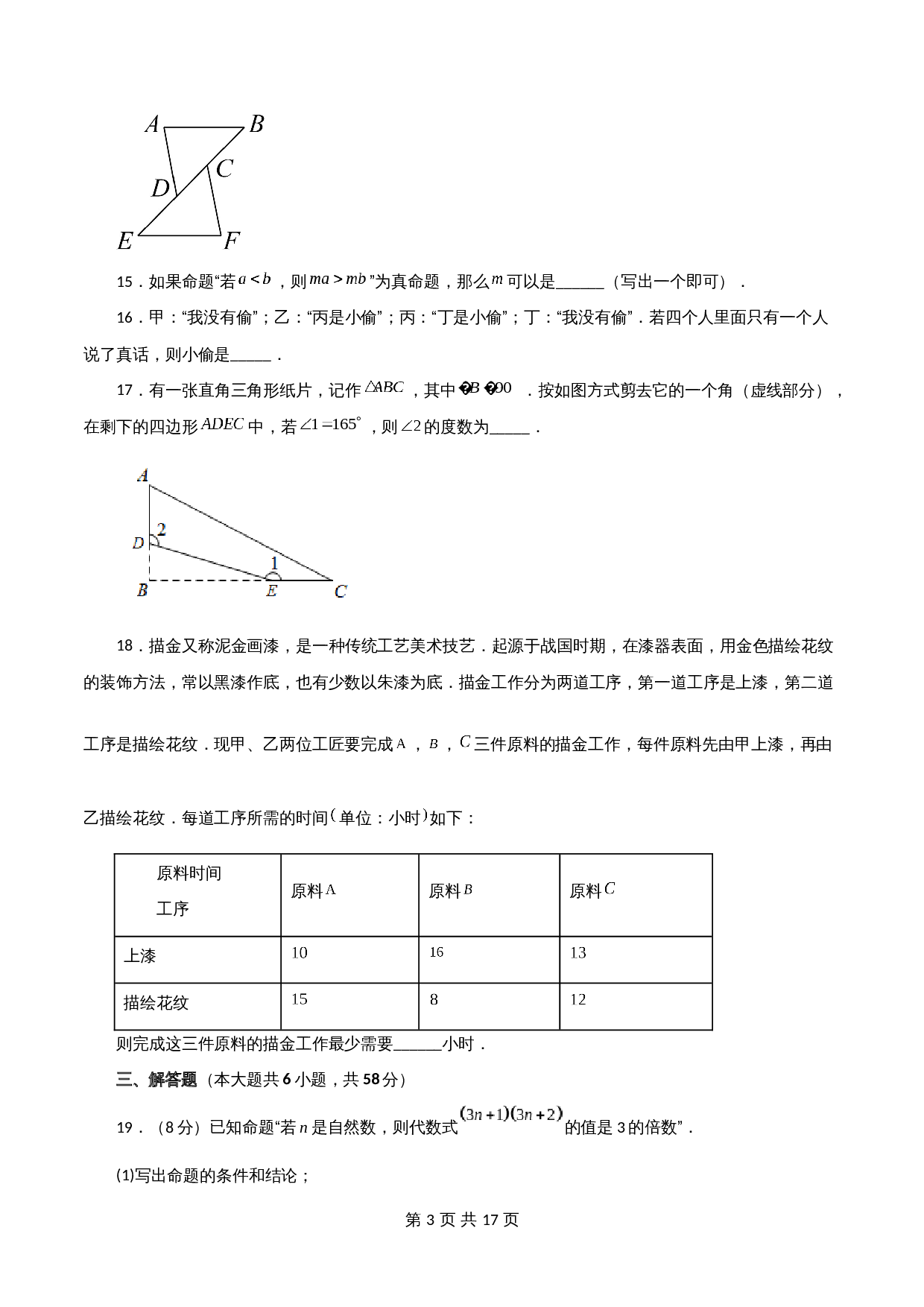 ④ 若 a ∥b ， b ∥ c ，则 a ∥ c ； ⑤ 两点确定一条直线． 12 ．有些真命题的逆命题也是真命题，在你学过的命题中，请写出一个这样的命题： ______ ． 13 ．已知下列命题： ① 若 ，则 ； ②2022 年全年鄂尔多斯 市一般 公共预算累计完成 亿元，用科学记数法表示为 元； ③ 二元一次方程 的 正整数解有 3 对 ； ④ 连接两点之间的线段叫做两点之间的距离．是真命题的是 ____________ ．（只填序号） 14 ．如图所示，已知 ， ， ．下列结论： ① ； ② ； ③ ．其中正确的结论是 ________ ．（填序号） 15 ．如果命题 “ 若 ，则 ” 为真命题，那么 可以是 ______ （写出一个即可）． 16 ．甲： “ 我没有偷 ” ；乙： “ 丙是小偷 ” ；丙： “ 丁是小偷 ” ；丁： “ 我没有偷 ” ．若四个人里面只有一个人说了真话，则小偷是 _____ ． 17 ．有一张直角三角形纸片，记作 ，其中 ．按如图方式剪去它的一个角（虚线部分），在剩下的四边形 中，若 ，则 的度数为 _____ ． 18 ．描金又称泥金画漆，是一种传统工艺美术技艺．起源于战国时期，在漆器表面，用金色描绘花纹的装饰方法，常以黑漆作底，也有少数以朱漆为底．描金工作分为两道工序，第一道工序是上漆，第二道工序是描绘花纹．现甲、乙两位工匠要完成 ， ， 三件原料的描金工作，每件原料先由甲上漆，再由乙描绘花纹．每道工序所需的时间 单位：小时 如下： 原料时间 工序 原料 原料 原料 上漆 描绘花纹 则完成这三件原料的描金工作最少需要 ______ 小时． 三、解答题 （本大题共 6 小题，共 58 分） 19 ． （ 8 分） 已知命题 “ 若 n 是自然数，则代数式 的值是 3 的倍数 ” ． (1) 写出命题的条件和结论； (2) 判断这个命题是真命题还是假命题，并说明理由． 20 ． （ 8 分） 如图，若 ，则直线 ．用推理的方法说明它是真命题． 21 ． （ 10 分） 补充完成下列证明过程，并填上推理的依据． 已知：如图， ．求证： ． 证明：延长 交 于点 ，则 ．（               ） 又 ∵ ， ∴ _______ ，（等量代换） ∴ ．（                     ） 22 ． （ 10 分） 如图，有如下四个论断： ① ； ② ； ③ 平分 ； ④ 平分 ，请你选择四个论断中的三个作为条件，余下的一个论断作为结论，构成一个正确的数学命题并证明它． 23 ． （ 10 分） 如图，有下列三个条件： ① DE // BC ； ② ； ③ ． (1) 若从这三个条件中任选两个作为题设，另一个作为结论，组成一个命题，