沪科版八年级下册数学试题 期末全真模拟试卷02（含答案）

期末全真模拟试卷 02 姓名 ：_ _________________ 班级 ：_ _____________ 得分 ：_ ________________ 一、选择题（本大题共 10 小题，每小题 3 分，共 30 分）在每小题所给出的四个选项中，只有一项是符合题目要求的． 1 ．代数式 在实数范围内有意义，则实数 x 的取值范围是（　　） A ． x ＞﹣ 1 B ． x ＜﹣ 1 C ． x ≤﹣ 1 D ． x ≥﹣ 1 2 ．如图，甲、乙、丙、丁四人手中各有一个圆形卡片，则卡片中的式子是分式的有（　　） A ． 1 个 B ． 2 个 C ． 3 个 D ． 4 个 3 ．若代数式 x 2 ﹣ 4 x + a 可化为（ x ﹣ b ） 2 ﹣ 1 ，则 a + b 是（　　） A ． 5 B ． 4 C ． 3 D ． 2 4 ．以下列各组数为三角形的边长，能构成直角三角形的是（　　） A ． 2 、 3 、 4 B ． 5 、 12 、 13 C ． 2 、 、 D ． 、 、 5 ．一组数据： 5 ， 6 ， 5 ， 3 ， 7 的众数是（　　） A ． 3 B ． 5 C ． 6 D ． 7 6 ．如图，在 ▱ ABCD 中， AB ＝ 4 ， BC ＝ 7 ，∠ ABC 的平分线 BE 交 AD 于点 E ，则 DE 的值是（　　） A ． 1 B ． 2 C ． 3 D ． 4 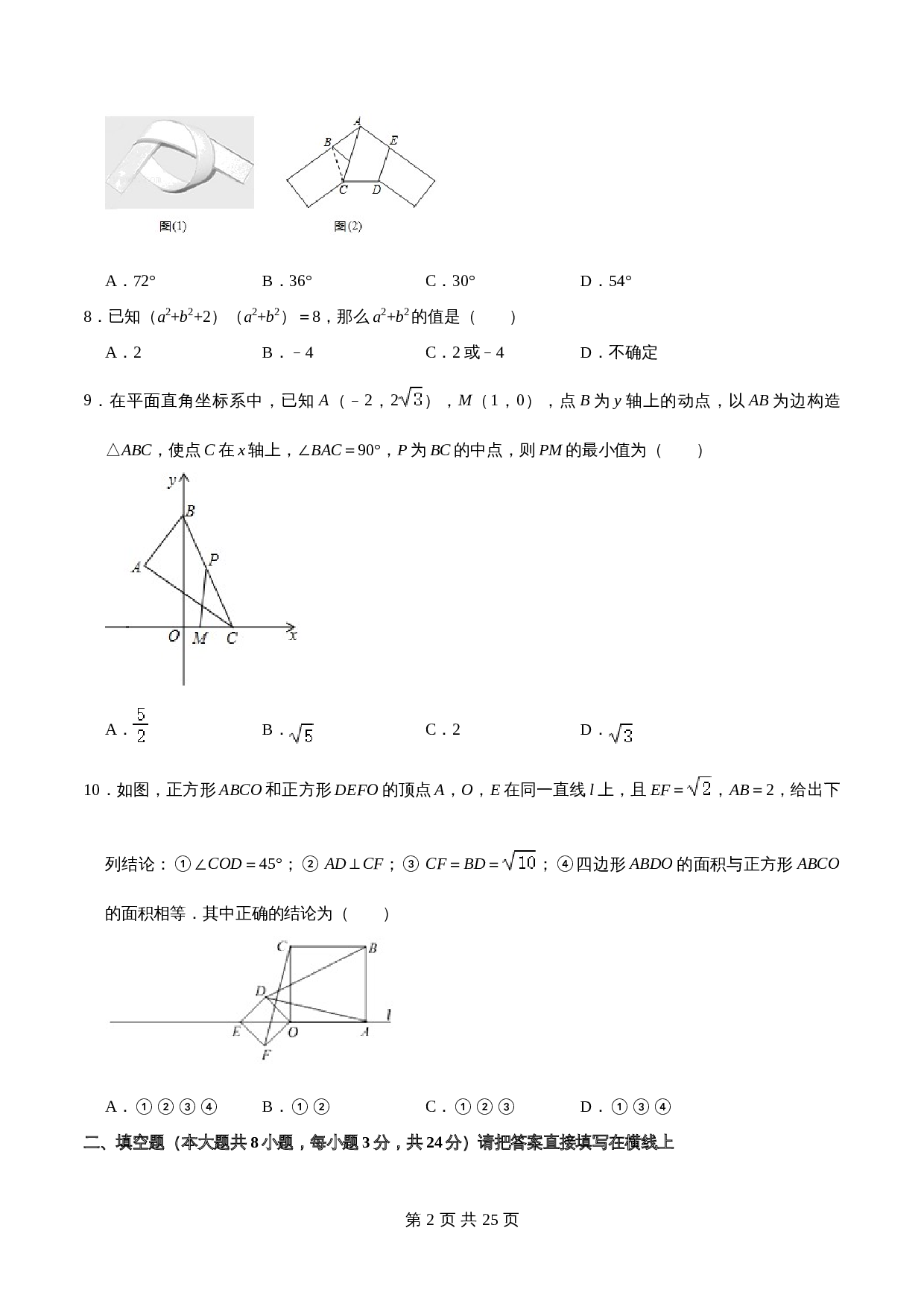7 ．如图，用一条宽度相等的足够长的纸条打一个结（如图 1 所示），然后轻轻拉紧、压平就可以得到如图 2 所示的正五边形 ABCDE ．图 2 中，∠ BAC 的大小是（　　） A ． 72 ° B ． 36 ° C ． 30 ° D ． 54 ° 8 ．已知（ a 2 + b 2 +2 ）（ a 2 + b 2 ）＝ 8 ，那么 a 2 + b 2 的值是（　　） A ． 2 B ．﹣ 4 C ． 2 或﹣ 4 D ．不确定 9 ．在平面直角坐标系中，已知 A （﹣ 2 ， 2 ）， M （ 1 ， 0 ），点 B 为 y 轴上的动点，以 AB 为边构造△ ABC ，使点 C 在 x 轴上，∠ BAC ＝ 90 °， P 为 BC 的中点，则 PM 的最小值为（　　） A ． B ． C ． 2 D ． 10 ．如图，正方形 ABCO 和正方形 DEFO 的顶点 A ， O ， E 在同一直线 l 上，且 EF ＝ ， AB ＝ 2 ，给出下列结论： ① ∠ COD ＝ 45 °； ② AD ⊥ CF ； ③ CF ＝ BD ＝ ； ④ 四边形 ABDO 的面积与正方形 ABCO 的面积相等．其中正确的结论为（　　） A ． ①②③④ B ． ①② C ． ①②③ D ． ①③④ 二、填空题（本大题共 8 小题，每小题 3 分，共 24 分）请把答案直接填写在横线上 11 ．计算： ＝ 　 　 ． 12 ．已知关于 x 方程 x 2 ﹣ 3 x + a ＝ 0 有一个根为 4 ，则方程的另一个根为 b ，则 a b ＝ 　 　 ． 13 ．在 ▱ ABCD 中，∠ A ＝ 30 °， AD ＝ 8 ， BD ＝ 8 ，则 ▱ ABCD 的面积等于 　 　 ． 14 ．已知一个多边形的每一个内角都是其相邻外角的 5 倍，则该多边形为 　 　 边形． 15 ．已知一组数据：﹣ 1 ， x ， 0 ， 1 ，﹣ 2 的平均数是 0 ，那么这组数据的方差为 　 　 ． 16 ．如图， A 、 B 、 C 、 D 均在正方形网格的格点上，则∠ ABC ﹣∠ DAC ＝ 　 　 °． 17 ．一个容器盛满纯药液 45 升，第一次倒出一部分纯药液后，用水加满；第二次又倒出同样多的药液，若此时容器内剩下的纯药液是 20 升，则每次倒出的液体是 　 　 升． 18 ．如图，在矩形 ABCD 中，边 AB ， AD 的长分别为 3 和 2 ，点 E 在 CD 上，点 F 在 AB 的延长线上，且 EC ＝ BF ，连接 FC ． （ 1 ）当 DE ＝ 2 时，则 FC 的长是 　 　 ； （ 2 ）点 E 在边 CD 上移动的过程中， AE + FC 的最小值是 　 　 ． 三、解答题（本大题共 7 小题，共 66 分．解答时应写出文字说明、证明过程或演算步骤） 19 ．（ 1 ）计算： 6 ﹣ 5 ﹣ +3 ． （ 2 ）计算： ﹣（ x + ）． （ 3 ）解方程： x 2 +4 x ﹣ 2 ＝ 0 ． 20 ．某学校开展了防溺水知识的宣传教育活动．为了解这次活动的效果，学校从全校 1500 名学生中随机抽取部分学生进行知识测试（测试满分 100 分，得分 x 均为不小于 60 的整数），并将测试成绩分为四个等级：基本合格（ 60 ≤ x ＜ 70 ），合格（ 70 ≤ x ＜ 80 ），良好（ 80 ≤ x ＜ 90 ），优秀（ 90 ≤ x ≤ 100 ），制作了统计图（部分信息未给出）． 根据图中给出的信息解答下列问题： （ 1 ）求测试成绩为合格的学生人数，并补全频数分布直方图； （ 2 ）这次测试成绩的中位数是什么等级？ （ 3 ）如果全校学生都参加测试，请你根据抽样测试的结果，估计该校获得优秀的学生有多少人？ 21 ．如图，四边形 ABCD 中， AB ⊥ BC ， AB ＝ BC ＝ 5 ， CD ＝ 7 ， AD ＝ 1 ． （ 1 ）求证：∠ ADC ＝ 90 °； （ 2 ）求△ ABD 的面积． 22 ．如图所示的正方形网格中，每个小正方形的边长都是 1 个单位长度，线段 AB 的端点 A ， B 都在正方形网格的格点上． （ 1 ）请在网格中画出平行四边形 ABCD ，使 AD ＝ （点 C ， D 都在正方形网格的格点上，画出一个符合题意的图形即可）； （ 2 ）在（ 1 ）中所画出的平行四边形 ABCD 的对角线 BD 的长是 　 　 ． 23 ．如图，四边形 ABCD 是菱形，对角线 AC ＝ 16 cm ， BD ＝ 12 cm ， DH ⊥ AB 于点 H ． （ 1 ）求菱形 ABCD 的周长； （ 2 ）求 DH 的长． 24 ．我们把一个式子或一个式子部分改写成完全平方式或者几个完全平方