2022-2023学年七年级数学下册期末模拟测试卷（江苏连云港专用）【满分冲刺卷】苏科版（含解析）

2022-2023七年级下册期末模拟测试卷 试卷满分：150分；考试时间：100分钟 班级： 姓名： 学号： 题号 一 二 三 总分 得分 第Ⅰ卷（选择题） 评卷人 得 分 选择题（共8小题，满分24分） 1．(本题3分)（2023·安徽合肥·合肥市第四十五中学校考模拟预测）下面计算正确的是（      ） A． B． C． D． 2．(本题3分)（2023春·山西临汾·八年级统考阶段练习）2022年12月，联发科正式发布了天玑8200处理器，天玑8200处理器采用台积电新一代4nm制程工艺，架构为1＋3＋4设计，性能核心最高主频达3.1GHz．已知1nm＝0.000000001m，则4nm用科学记数法可表示为（      ）m A． B． C． D． 3．(本题3分)（2023秋·浙江湖州·八年级统考期末）已知 ，则下列不等式中正确的是 （      ） A． B． C． D． 4．(本题3分)（2023春·福建福州·七年级福建省福州第十九中学校考期中）下列命题是假命题的是（      ） A．等角的补角相等 B．垂线段最短 C．两点之间，线段最短 D．无限小数是无理数 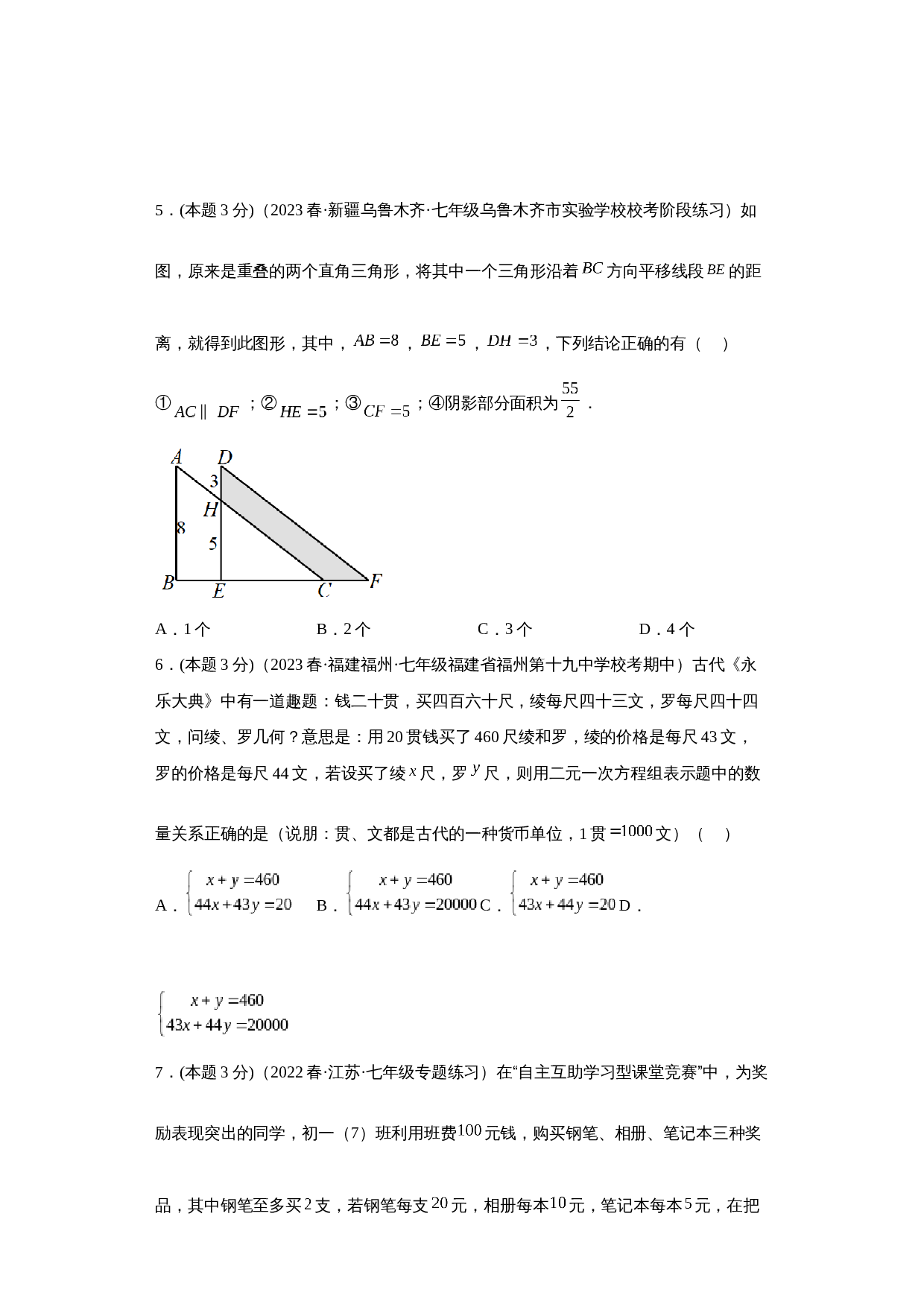5．(本题3分)（2023春·新疆乌鲁木齐·七年级乌鲁木齐市实验学校校考阶段练习）如图，原来是重叠的两个直角三角形，将其中一个三角形沿着 方向平移线段 的距离，就得到此图形，其中， ， ， ，下列结论正确的有（      ） ① ；② ；③ ；④阴影部分面积为 ． A．1个 B．2个 C．3个 D．4个 6．(本题3分)（2023春·福建福州·七年级福建省福州第十九中学校考期中）古代《永乐大典》中有一道趣题：钱二十贯，买四百六十尺，绫每尺四十三文，罗每尺四十四文，问绫、罗几何？意思是：用20贯钱买了460尺绫和罗，绫的价格是每尺43文，罗的价格是每尺44文，若设买了绫 尺，罗 尺，则用二元一次方程组表示题中的数量关系正确的是（说朋：贯、文都是古代的一种货币单位，1贯 文）（      ） A． B． C． D． 7．(本题3分)（2022春·江苏·七年级专题练习）在“自主互助学习型课堂竞赛”中，为奖励表现突出的同学，初一（7）班利用班费 元钱，购买钢笔、相册、笔记本三种奖品，其中钢笔至多买 支，若钢笔每支 元，相册每本 元，笔记本每本 元，在把钱都用尽的条件下，买法共有（      ） A． 种 B． 种 C． 种 D． 种 8．(本题3分)（2019春·七年级课时练习）如图，在长方形 ABCD 中， AB ＝ 2cm ， AD ＝ 4cm ， E ， F 分别为 AD ， BC 的中点，分别以 C ， F 为圆心、 2cm 为半径画图把长方形分成三个部分，则图中两个阴影部分的面积为(　　) A．2cm 2 B．4cm 2 C．6cm 2 D．无法确定 第Ⅱ卷（非选择题） 评卷人 得 分 填空题（共8小题，满分24分） 9．(本题3分)（2023春·江苏无锡·九年级校考阶段练习）命题“如果 ，那么 ”的逆命题是：_______． 10．(本题3分)（2021春·八年级课时练习） 不等式 5 ﹣ 2 x ＜ 1 的解集为 _____ ． 11．(本题3分)（2023春·全国·七年级期中）若 ， ， 为 的三边长，化简： _________． 12．(本题3分)（2023春·江苏·七年级期中）一个多边形的外角和是内角和的一半，则这个多边形的边数为___________． 13．(本题3分)（2023春·山东济南·七年级校考阶段练习）若 ， ，则代数式 的值是______． 14．(本题3分)（2022春·江苏无锡·七年级校考阶段练习）如图，在 中， D ， E 分别是 的中点，点 F 在 上，且 ，若 ，则 等于______． 15．(本题3分)（2023秋·四川眉山·八年级统考期末）若 ， ______． 16．(本题3分)（2022秋·八年级课时练习）在 中， ，点 D 在 内，将射线 沿直线 翻折，将射线 沿直线 翻折，两射线交于点 E ，若 ，则 的度数为________． 评卷人 得 分 三．解答题（共11小题，满分102分） 17．(本题8分)（2023春·江苏无锡·七年级无锡市太湖格致中学校考阶段练习）计算： (1) (2) ． 18．(本题8分)（2023春·全国·八年级专题练习）分解因式： (1) (2) (本题8分)（2023春·浙江·七年级专题练习）先化简再求值： ，其中 ． （1） 解方程组： （2） 解不等式组： 2 1 ．(本题8分)（2023春·七年级单元测试）（1）如图，已知∠ A ＝∠ C ，若 AB // CD ，则 BC // AD ．请说明理由． 理由如下： ∵ AB // CD （已知）， ∴∠ ABE ＝∠______（______）． ∵∠ A ＝∠ C （已知）， ∴______（______）． ∴ BC // AD （_______）． （2）请写出问题（1）的逆命题，并判断它是真命题还是假命题，真命题请写出证明过程，假命题举出反例． 2 2 ．(本题8分)（2023春·重庆北碚·七年级西南大学附中校考期中）关于 x ， y 的方程组 的解满足 x 为非正数， y 为正数． (1)求 a 的取值范围； (2)已知不等式 的解集为 ，请求出所有满足条件的整数 a 的值． 23 ．(本题10分)（2023春·江苏泰州·七年级校考阶段练习）如图， 中， 于点 ， ， 平分 交 于 ， ． (1)求 的度数； (2)若点 F 为线段 上的任意一点，当 为直角三角形时，求 的度数． 2 4 ．(本题10分)（2022秋·广西南宁·八年级南宁十四中校考开学考试）某学校计划购买 、 两种型号的空调，经调研得知：购买 台 型空调和 台 型空调共需 元，购买