【达标突破】苏科版八年级上册数学 期末考试卷（B卷·强化提升）（含解析）

苏科版数学八年级上学期期末考试卷 （ B 卷·强化提升） （原卷版） 学校 :___________ 姓名： ___________ 班级： ___________ 考号： ___________ 一、单选题 ( 每小题 2 分，共 16 分 ) 1 ．（ 2021· 江苏海陵 · 八年级期末）点 P 坐标为（ m ＋ 1 ， m － 2 ），则点 P 不可能在（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 2 ．（ 2021· 江苏无锡 · 八年级期末）如图，已知一次函数 y ＝ kx + b 的 图象 经过点 A （﹣ 1 ， 2 ）和点 B （﹣ 2 ， 0 ），一次函数 y ＝ mx 的 图象 经过点 A ，则关于 x 的不等式组 0 ＜ kx + b ＜ mx 的解集为（　　） A ．﹣ 2 ＜ x ＜﹣ 1 B ．﹣ 1 ＜ x ＜ 0 C ． x ＜﹣ 1 D ． x ＞﹣ 1 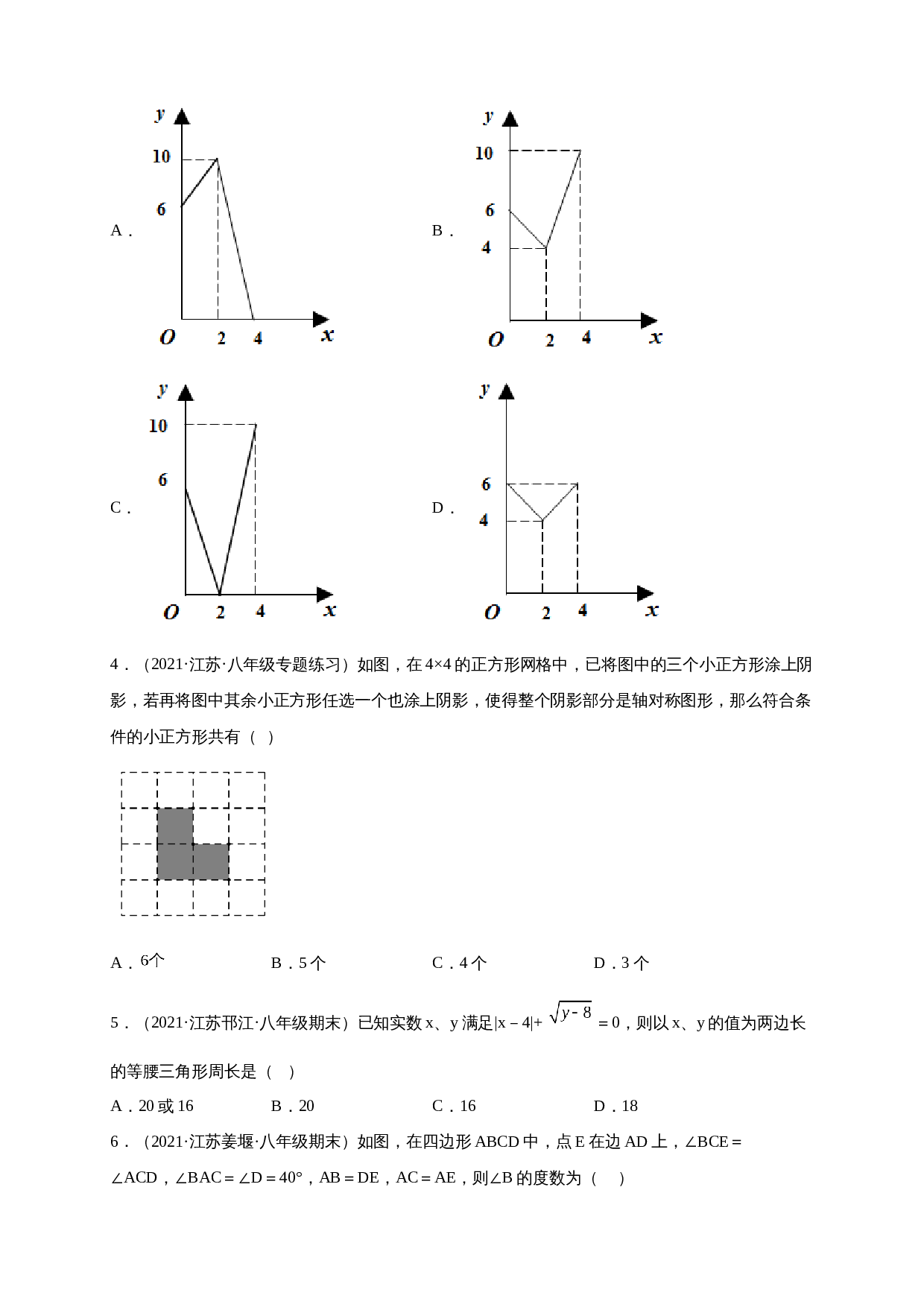3 ．（ 2021· 江苏苏州 · 八年级期末）在数轴上，点 表示－ 2 ，点 表示 为数轴上两点，点 从点 出发以每秒 个 单位长度的速度向左运动，同时点 从点 出发以每秒 个 单位长度的速度向左运动，点 到达原点 后，立即以原来的速度返回，当点 回到点 时，点 与点 同时停止运动．设点 运动的时间为 秒，点 与点 之间的距离为 个 单位长度，则下列图像中表示 与 的函数关系的是（ ） A ． B ． C ． D ． 4 ．（ 2021· 江苏 · 八年级专题练习）如图，在 4×4 的正方形网格中，已将图中的三个小正方形涂上阴影，若再将图中 其余小 正方形任选一个也涂上阴影，使得整个阴影部分是轴对称图形，那么符合条件的小正方形共有（ ） A ． B ． 5 个 C ． 4 个 D ． 3 个 5 ．（ 2021· 江苏邗江 · 八年级期末）已知实数 x 、 y 满足 |x － 4|+ ＝ 0 ，则以 x 、 y 的值为两边长的等腰三角形周长是（ ） A ． 20 或 16 B ． 20 C ． 16 D ． 18 6 ．（ 2021· 江苏姜堰 · 八年级期末）如图，在四边形 ABCD 中，点 E 在边 AD 上， ∠BCE ＝ ∠ACD ， ∠BAC ＝ ∠D ＝ 40° ， AB ＝ DE ， AC ＝ AE ，则 ∠B 的度数为（ ） A ． 100° B ． 110° C ． 120° D ． 130° 7 ．（ 2021· 江苏 · 无锡市东林 中学八 年级期中）如图，在 ADE 和 ABC 中， ∠ E ＝ ∠ C ， DE ＝ BC ， EA ＝ CA ，过 A 作 AF ⊥ DE ，垂足为 F ， DE 交 CB 的延长线于点 G ，连接 AG ．四边形 DGBA 的面积为 12 ， AF ＝ 4 ，则 FG 的长是（　　） A ． 2 B ． 2.5 C ． 3 D ． 8 ．（ 2021· 江苏海安 · 八年级期末）如图，在 中， 平分 ．边 的垂直平分线 分别交 于点 ．以下说法错误的是（ ） A ． B ． C ． D ． 二、填空题 ( 每小题 2 分，共 16 分 ) 9 ．（ 2021· 江苏广陵 · 八年级期末）如图，直线 与直线 相交于点 ，则方程组 的解是 ______ ． 10 ．（ 2021· 江苏广陵 · 八年级期末）已知函数 ， ， ， 若无论 取何值， 总取 ， ， 中的最大值，则 的最小值是 ______ ． 11 ．（ 2021· 江苏高邮 · 八年级期末）如图，在 中，线段 的垂直平分线交 于点 ，连接 ，若 ， ，则 的度数为 _____° ． 12 ．（ 2021· 江苏广陵 · 八年级期末）课间操时，小明、小丽、小亮的位置如图所示，如果小明的位置用 表示，小丽的位置用 表示，那么小亮的位置可以表示成 ______ ． 13 ．（ 2021· 江苏苏州 · 八年级期末）比较大小： _____________ （填 “ ＞ ” 、 “ ＝ ” 或 “ ＜ ” ）． 14 ．（ 2021· 江苏常州 · 八年级期末）《九章算术》中有一个 “ 折竹抵地 ” 问题： “ 今有竹高九尺，末折抵地，去本三尺，问折者高几何？ ” 意思是：现有竹子高 9 尺，折 后竹尖抵地 与竹子底部的距离为 3 尺， 问折处 高几尺？即：如图， AB ＋ AC ＝ 9 尺， BC ＝ 3 尺，则 AC =_____ 尺． 15 ．（ 2021· 江苏如皋 · 八年级期末）如图， 中， ， ，点 为 边上一动点．分别作点 关于 ， 的对称点 ， ，连接 ， ．则 的度数等于 _______ ． 16 ．（ 2021· 江苏昆山 · 八年级期末）如图， ，点 、 、 、 在同一条直线上， 、 交于点 ， ，则 的度数是 ______° ． 三、解答题 ( 共 68 分 ) 17 ． ( 本题 6 分 ) （ 2021· 江苏广陵 · 八年级期末）（ 1 ）计算： ； （ 2 ）求满足条件的 值： ． 18 ． ( 本题 6 分 ) （ 2021· 江苏东台 · 八年级期末）一艘轮船从 A 港向南偏西 48° 方向航行 100km 到达 B 岛，再从 B 岛沿 BM 方向航行 125km 到达 C 岛， A 港到航线 BM 的最短距离是 60km ． （ 1 ）若轮船速度为 25km/ 小时，求轮船从 C 岛沿 CA 返回 A 港所需的时间． （ 2 ） C 岛在 A 港的什么方向？ 19 ． ( 本题 8 分 ) （ 2021· 江苏江阴 · 八年级期末）先化简 ，再从不等式组 的整数解中选一个合适的 的值代入求值． 20 ． ( 本题 6 分 ) （ 2021· 江苏仪征 · 八年级期末）（直观想象）如图 1 ，动点 P 在数轴上从负半轴向正半轴运动，点 P 到原点的距离先变小再变大，当点 P 的位置确定时，点 P 到原点的距离也唯一确定； （数学发现）当一个动点 P （ x ， 0 ）到一个定点的距离为 d ，我们发现 d 是 x 的函数； （数学理解）（ 1 ）动点 P （ x ， 0 ）到定点 A （ 2 ， 0 ）的距离为 d ，当 x ＝