【压轴题】专题24以三角形为载体的几何综合问题 （全国通用）（含解析）-2024年中考数学复习

2024年中考数学压轴题之学霸秘笈大揭秘（全国通用） 专题24以三角形为载体的几何综合问题 【 例1】 （2022·山东枣庄·中考真题）已知△ ABC 中，∠ ACB ＝90°， AC ＝ BC ＝4cm，点 P 从点 A 出发，沿 AB 方向以每秒 cm的速度向终点 B 运动，同时动点 Q 从点 B 出发沿 BC 方向以每秒1cm的速度向终点 C 运动，设运动的时间为 t 秒． (1)如图①，若 PQ ⊥ BC ，求 t 的值； (2)如图②，将△ PQC 沿 BC 翻折至△ P ′ QC ，当 t 为何值时，四边形 QPCP ′为菱形？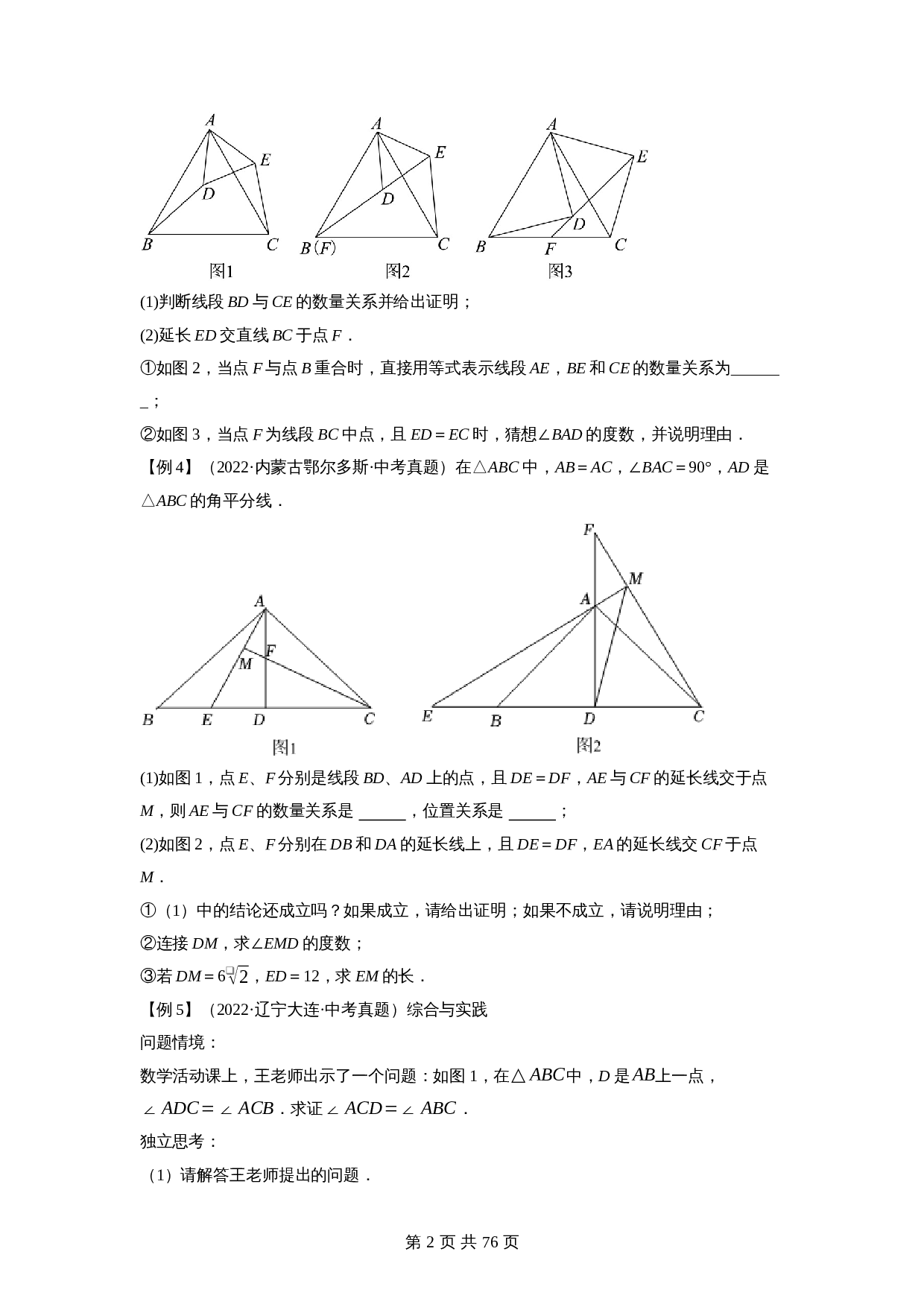 【 例2】 （2022·山东菏泽·中考真题）如图1，在 中， 于点 D ，在 DA 上取点 E ，使 ，连接 BE 、 CE ． (1)直接写出 CE 与 AB 的位置关系； (2)如图2，将 绕点 D 旋转，得到 （点 ， 分别与点 B ， E 对应），连接 ，在 旋转的过程中 与 的位置关系与（1）中的 CE 与 AB 的位置关系是否一致?请说明理由； (3)如图3，当 绕点 D 顺时针旋转30°时，射线 与 AD 、 分别交于点 G 、 F ，若 ，求 的长． 【 例3】 （2022·山东济南·中考真题）如图1，△ ABC 是等边三角形，点 D 在△ ABC 的内部，连接 AD ，将线段 AD 绕点 A 按逆时针方向旋转60°，得到线段 AE ，连接 BD ， DE ， CE ． (1)判断线段 BD 与 CE 的数量关系并给出证明； (2)延长 ED 交直线 BC 于点 F ． ①如图2，当点 F 与点 B 重合时，直接用等式表示线段 AE ， BE 和 CE 的数量关系为_______； ②如图3，当点 F 为线段 BC 中点，且 ED ＝ EC 时，猜想∠ BAD 的度数，并说明理由． 【 例4】 （2022·内蒙古鄂尔多斯·中考真题）在△ ABC 中， AB ＝ AC ，∠ BAC ＝90°， AD 是△ ABC 的角平分线． (1)如图1，点 E 、 F 分别是线段 BD 、 AD 上的点，且 DE ＝ DF ， AE 与 CF 的延长线交于点 M ，则 AE 与 CF 的数量关系是 　 　 ，位置关系是 　 　 ； (2)如图2，点 E 、 F 分别在 DB 和 DA 的延长线上，且 DE ＝ DF ， EA 的延长线交 CF 于点 M ． ①（1）中的结论还成立吗？如果成立，请给出证明；如果不成立，请说明理由； ②连接 DM ，求∠ EMD 的度数； ③若 DM ＝6 ， ED ＝12，求 EM 的长． 【 例5】 （2022·辽宁大连·中考真题）综合与实践 问题情境： 数学活动课上，王老师出示了一个问题：如图1，在 中， D 是 上一点， ．求证 ． 独立思考： （1）请解答王老师提出的问题． 实践探究： （2）在原有问题条件不变的情况下，王老师增加下面的条件，并提出新问题，请你解答．“如图2，延长 至点 E ，使 ， 与 的延长线相交于点 F