2024年中考数学压轴题之学霸秘笈大揭秘(全国通用)
专题28以圆为载体的几何综合问题
【
例1】
(2022·河北·育华中学三模)如图,在四边形
ABCD
中,∠
A
=∠
B
=90°,
AD
=4,
BC
=10,sin
C
=
,以
AB
为直径作⊙
O
,把⊙
O
沿水平方向平移
x
个单位,得到⊙
O
′,
A
'
B
'为直径
AB
平移后的对应线段.
(1)当
x
=0,且
M
为⊙
O
上一点时,求
DM
的最大值;
(2)当
B
′与
C
重合时,设⊙
O
′与
CD
相交于点
N
,求点
N
到
AB
的距离;
(3)当⊙
O
′与
CD
相切时,直接写出
x
的值
.
【
例2】
(2022·黑龙江哈尔滨·中考真题)已知
是
的直径,点
A
,点
B
是
上的两个点,连接
,点
D
,点
E
分别是半径
的中点,连接
,且
.
(1)如图1,求证:
;
(2)如图2,延长
交
于点
F
,若
,求证:
;
(3)如图3,在(2)的条件下,点
G
是
上一点,连接
,若
,
,求
的长.
【
例3】
(2022·黑龙江绥化·中考真题)如图所示,在
的内接
中,
,
,作
于点
P
,交
于另一点
B
,
C
是
上的一个动点(不与
A
,
M
重合),射线
交线段
的延长线于点
D
,分别连接
和
,
交
于点
E
.
(1)求证:
.
(2)若
,
,求
的长.
(3)在点
C
运动过程中,当
时,求
的值.
【
例4】
(2022·湖北荆州·中考真题)如图1,在矩形
ABCD
中,
AB
=4,
AD
=3,点
O
是边
AB
上一个动点(不与点
A
重合),连接
OD
,将△
OAD
沿
OD
折叠,得到△
OED
;再以
O
为圆心,
OA
的长为半径作半圆,交射线
AB
于
G
,连接
AE
并延长交射线
BC
于
F
,连接
EG
,设
OA
=
x
.
(1)求证:
DE
是半圆
O
的切线;
(2)当点
E
落在
BD
上时,求
x
的值;
(3)当点
E
落在
BD
下方时,设△
AGE
与△
AFB
面积的比值为
y
,确定
y
与
x
之间的函数关系式;
(4)
直接写出
:当半圆
O
与△
BCD
的边有两个交点时,
x
的取值范围.
25.(2022·浙江温州·中考真题)如图1,
为半圆
O
的直径,
C
为
延长线上一点,
切半圆于点
D
,
,交
延长线于点
E
,交半圆于点
F
,已知
.点
P
,
Q
分别在线段
上(不与端点重合),且满足
.设
.
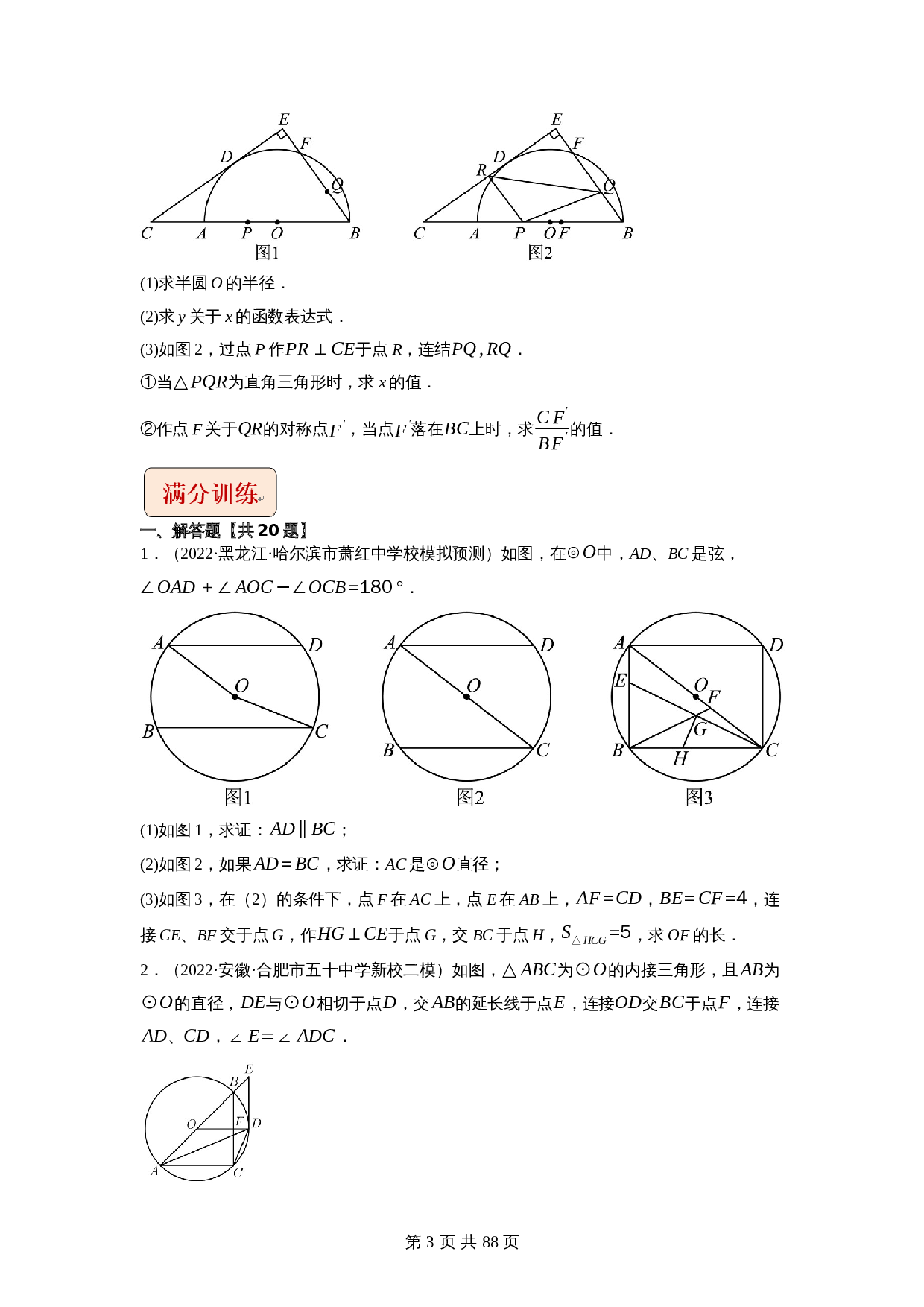
(1)求半圆
O
的半径.
(2)求
y
关于
x
的函数表达式.
(3)如图2,过点
P
作
于点
R
,连结
.
①当
为直角三角形时,求
x
的值.
②作点
F
关于
的对称点
,当点
落在
上时,求
的值.
一、解答题
【
共20题】
1.(2022·黑龙江·哈尔滨市萧红中学校模拟预测)如图,在
中,
AD
、
BC
是弦,
.
(1)如图1,求证:
;
(2)如图2,如果
,求证:
AC
是
直
【压轴题】专题28以圆为载体的几何综合问题(全国通用)(含解析)-2024年中考数学复习