【压轴题】专题32四边形与新定义综合问题 （全国通用）（含解析）-2024年中考数学复习

2024年中考数学压轴题之学霸秘笈大揭秘（全国通用） 专题32四边形与新定义综合问题 【 例1】 （2022•汇川区模拟）定义：有一组对角互补的四边形叫做“对补四边形”，例如：四边形 ABCD 中，若∠ A +∠ C ＝180°或∠ B +∠ D ＝180°，则四边形 ABCD 是“对补四边形”． 【概念理解】（1）如图1，四边形 ABCD 是“对补四边形”． ① 若∠ A ：∠ B ：∠ C ＝3：2：1，则∠ D ＝ 　 　 度． ② 若∠ B ＝90°．且 AB ＝3， AD ＝2时．则 CD 2 ﹣ CB 2 ＝ 　 　 ． 【类比应用】（2）如图2，在四边形 ABCD 中， AB ＝ CB ， BD 平分∠ ADC ．求证：四边形 ABCD 是“对补四边形”． 【 例2】 ．（2022•赣州模拟）我们定义：有一组邻角相等的凸四边形做“等邻角四边形”，例如：如图1，∠ B ＝∠ C ，则四边形 ABCD 为等邻角四边形． （1）定义理解：已知四边形 ABCD 为等邻角四边形，且∠ A ＝130°，∠ B ＝120°，则∠ D ＝ 　 　 度． （2）变式应用：如图2，在五边形 ABCDE 中， ED ∥ BC ，对角线 BD 平分∠ ABC ． ① 求证：四边形 ABDE 为等邻角四边形； ② 若∠ A +∠ C +∠ E ＝300°，∠ BDC ＝∠ C ，请判断△ BCD 的形状，并明理由． （3）深入探究：如图3，在等邻角四边形 ABCD 中，∠ B ＝∠ BCD ， CE ⊥ AB ，垂足为 E ，点 P 为边 BC 上的一动点，过点 P 作 PM ⊥ AB ， PN ⊥ CD ，垂足分别为 M ， N ．在点 P 的运动过程中，判断 PM + PN 与 CE 的数量关系？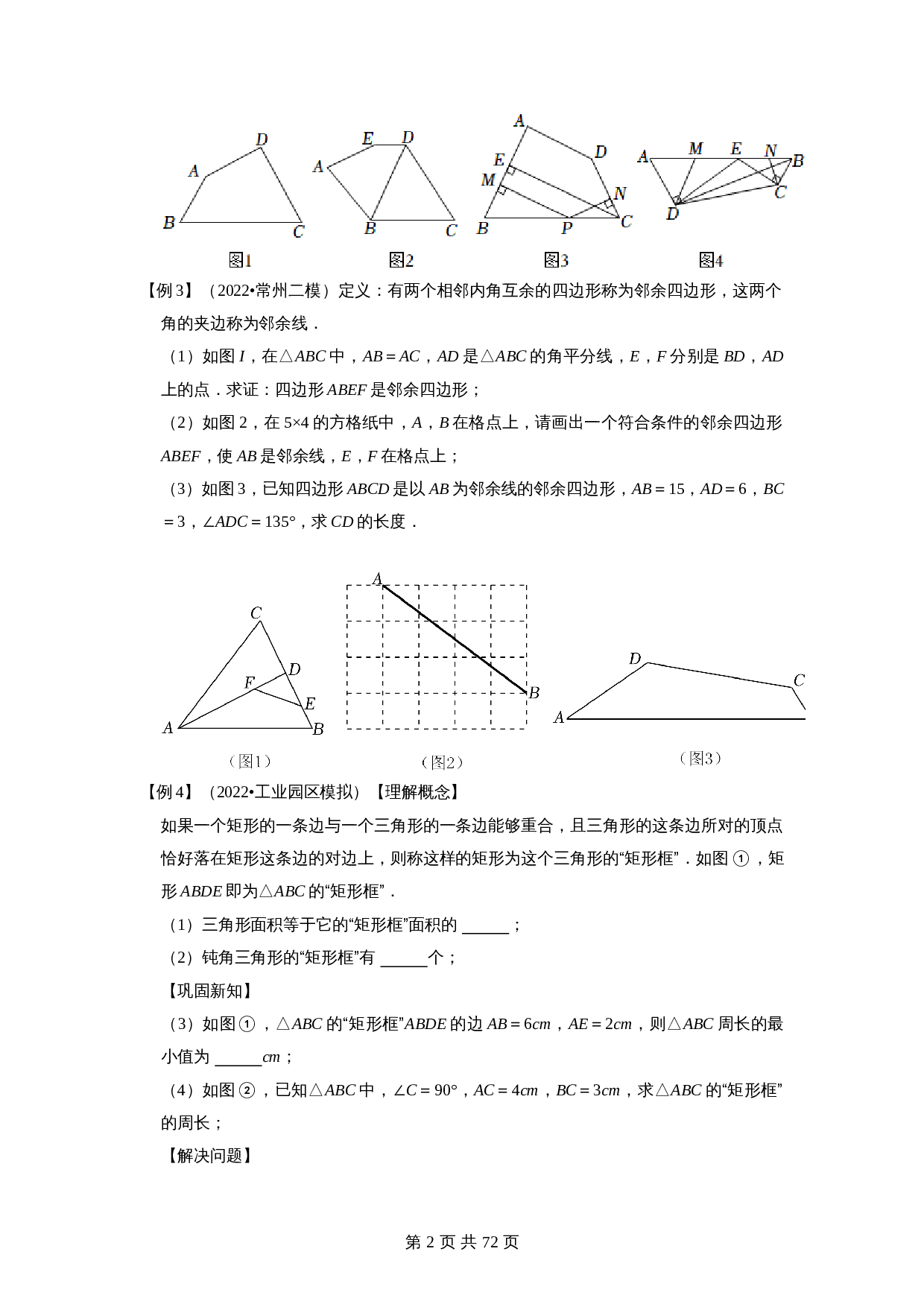请说明理由． （4）迁移拓展：如图4，是一个航模的截面示意图．四边形 ABCD 是等邻角四边形，∠ A ＝∠ ABC ， E 为 AB 边上的一点， ED ⊥ AD ， EC ⊥ CB ，垂足分别为 D 、 C ， AB ＝2 dm ， AD ＝3 dm ， BD ＝ dm ． M 、 N 分别为 AE 、 BE 的中点，连接 DM 、 CN ，求△ DEM 与△ CEN 的周长之和． 【 例3】 （2022•常州二模）定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线． （1）如图 I ，在△ ABC 中， AB ＝ AC ， AD 是△ ABC 的角平分线， E ， F 分别是 BD ， AD 上的点．求证：四边形 ABEF 是邻余四边形； （2）如图2，在5×4的方格纸中， A ， B 在格点上，请画出一个符合条件的邻余四边形 ABEF ，使 AB 是邻余线， E ， F 在格点上； （3）如图3，已知四边形 ABCD 是以 AB 为邻余线的邻余四边形， AB ＝15， AD ＝6， BC ＝3，∠ ADC ＝135°，求 CD 的长度． 【 例4】 （2022•工业园区模拟）【理解概念】 如果一个矩形的一条边与一个三角形的一条边能够重合，且三角形的