【压轴题】专题21二次函数与三角函数综合问题（全国通用）（含解析）-2024年中考数学复习

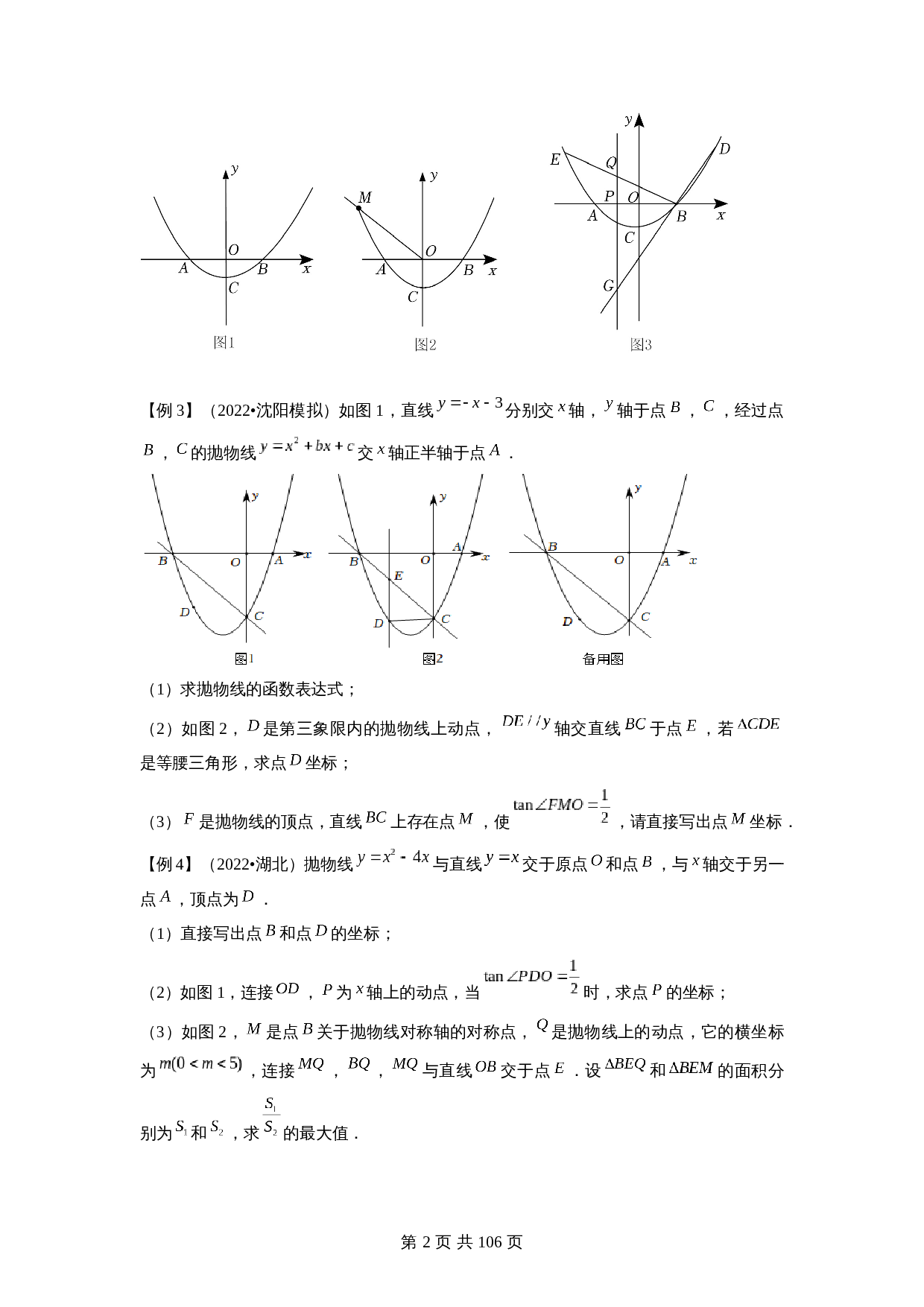
2024年中考数学压轴题之学霸秘笈大揭秘（全国通用） 专题21二次函数与三角函数综合问题 【 例1】 （2022•泰安二模）抛物线 的顶点 在 轴上，与 轴交于点 ． （ 1 ）求抛物线的解析式； （ 2 ）如图 1 ，直线 交抛物线于 ， 两点，若 ，求 的面积； （ 3 ）如图 2 ，已知（ 2 ）中 点坐标，点 是第二象限抛物线上一点，是否存在点 ，使得 ，若存在，请求出点 坐标，若不存在，请说明理由． 【例2】（2022•江岸区校级模拟）抛物线 与 轴交于 、 两点，与 轴交于 点，且 ， ． （ 1 ）如图 1 ，求抛物线的解析式； （ 2 ）如图 2 ，若 ， 是抛物线上两点， 在对称轴右侧，且 ，求 点坐标； （ 3 ）如图 3 ， 是 点右侧抛物线上的一动点， 、 两点关于 轴对称，直线 、 分别交直线 于 、 两点， 交 轴于 ，求 的值． 【例3】（2022•沈阳模拟）如图 1 ，直线 分别交 轴， 轴于点 ， ，经过点 ， 的抛物线 交 轴正半轴于点 ． （ 1 ）求抛物线的函数表达式； （ 2 ）如图 2 ， 是第三象限内的抛物线上动点， 轴交直线 于点 ，若 是等腰三角形，求点 坐标； （ 3 ） 是抛物线的顶点，直线 上存在点 ，使 ，请直接写出点 坐标． 【例4】（2022•湖北）抛物线 与直线 交于原点 和点 ，与 轴交于另一点 ，顶点为 ． （ 1 ）直接写出点 和点 的坐标； （ 2 ）如图 1 ，连接 ， 为 轴上的动点，当 时，求点 的坐标； （ 3 ）如图 2 ， 是点 关于抛物线对称轴的对称点， 是抛物线上的动点，它的横坐标为 ，连接 ， ， 与直线 交于点 ．设 和 的面积分别为 和 ，求 的最大值． 【例5】（2022•南充）抛物线 与 轴分别交于点 ， ，与 轴交于点 ． （ 1 ）求抛物线的解析式． （ 2 ）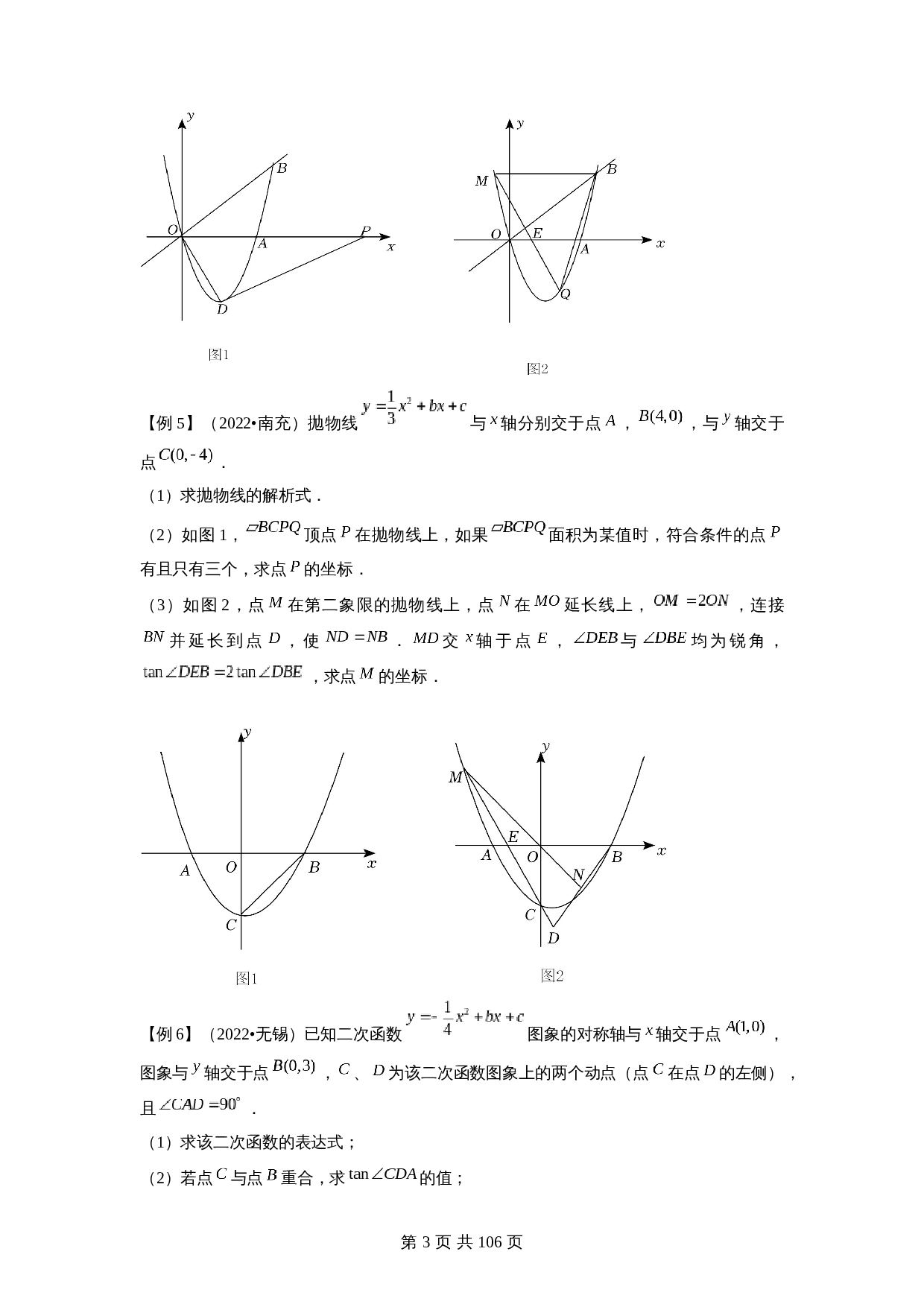如图 1 ， 顶点 在抛物线上，如果 面积为某值时，符合条件的点 有且只有三个，求点 的坐标． （ 3 ）如图 2 ，点 在第二象限的抛物线上，点 在 延长线上， ，连接 并延长到点 ，使 ． 交 轴于点 ， 与 均为锐角， ，求点 的坐标． 【例6】（2022•无锡）已知二次函数 图象的对称轴与 轴交于点 ，图象与 轴交于点 ， 、 为该二次函数图象上的两个动点（点 在点 的左侧），且 ． （ 1 ）求该二次函数的表达式； （ 2 ）若点 与点 重合，求 的值； （ 3 ）点 是否存在其他的位置，使得 的值与（ 2 ）中所求的值相等？若存在，请求出点 的坐标；若不存在，请说明理由． 一．解答题（共2 0 题） 1．（2022秋•工业园区期中）已知抛物线 的图象与 轴交于 、 两点（点 在点 的左侧），