【压轴题】专题33圆与新定义综合问题 （全国通用）（含解析）-2024年中考数学复习

2024年中考数学压轴题之学霸秘笈大揭秘（全国通用） 专题33圆与新定义综合问题 【 例1】 （2022•石景山区一模）在平面直角坐标系 xOy 中，点 P 不在坐标轴上，点 P 关于 x 轴的对称点为 P 1 ，点 P 关于 y 轴的对称点为 P 2 ，称△ P 1 PP 2 为点 P 的“关联三角形”． （1）已知点 A （1，2），求点 A 的“关联三角形”的面积； （2）如图，已知点 B （ m ， m ）， ⊙ T 的圆心为 T （2，2），半径为2．若点 B 的“关联三角形”与 ⊙ T 有公共点，直接写出 m 的取值范围； （3）已知 ⊙ O 的半径为 r ， OP ＝2 r ，若点 P 的“关联三角形”与 ⊙ O 有四个公共点，直接写出∠ PP 1 P 2 的取值范围． 【 例2】 2022•朝阳区二模）在平面直角坐标系 xOy 中， ⊙ O 的半径为1， AB ＝1，且 A ， B 两点中至少有一点在 ⊙ O 外．给出如下定义：平移线段 AB ，得到线段 A ′ B ′（ A ′， B ′分别为点 A ， B 的对应点），若线段 A ′ B ′上所有的点都在 ⊙ O 的内部或 ⊙ O 上，则线段 AA ′长度的最小值称为线段 AB 到 ⊙ O 的“平移距离”． （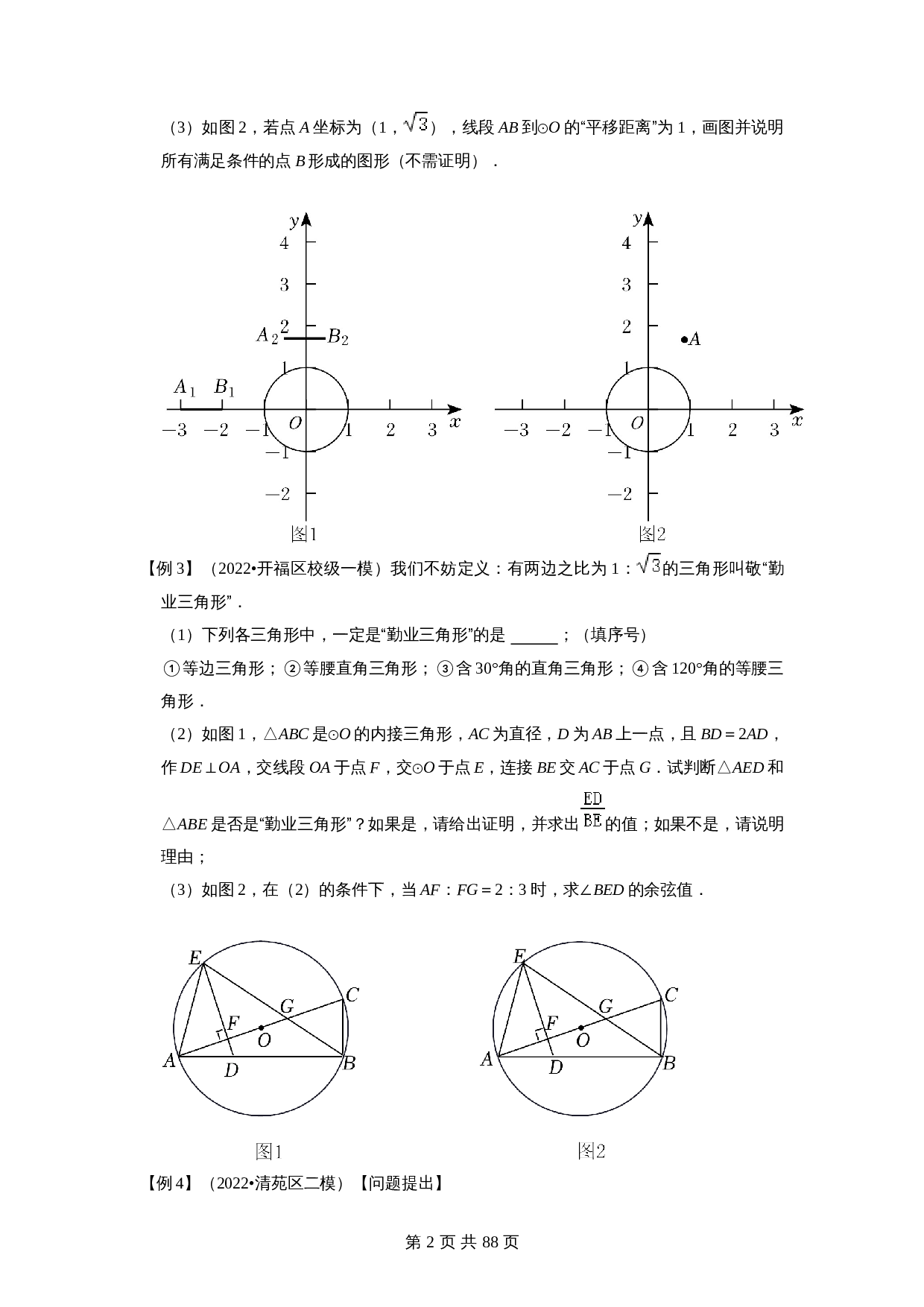1）如图1，点 A 1 ， B 1 的坐标分别为（﹣3，0），（﹣2，0），线段 A 1 B 1 到 ⊙ O 的“平移距离”为 　 　 ，点 A 2 ， B 2 的坐标分别为（﹣ ， ），（ ， ），线段 A 2 B 2 到 ⊙ O 的“平移距离”为 　 　 ； （2）若点 A ， B 都在直线 y ＝ x +2 上，记线段 AB 到 ⊙ O 的“平移距离”为 d ，求 d 的最小值； （3）如图2，若点 A 坐标为（1， ），线段 AB 到 ⊙ O 的“平移距离”为1，画图并说明所有满足条件的点 B 形成的图形（不需证明）． 【 例3】 （2022•开福区校级一模）我们不妨定义：有两边之比为1： 的三角形叫敬“勤业三角形”． （1）下列各三角形中，一定是“勤业三角形”的是 　 　 ；（填序号） ① 等边三角形； ② 等腰直角三角形； ③ 含30°角的直角三角形； ④ 含120°角的等腰三角形． （2）如图1，△ ABC 是 ⊙ O 的内接三角形， AC 为直径， D 为 AB 上一点，且 BD ＝2 AD ，作 DE ⊥ OA ，交线段 OA 于点 F ，交 ⊙ O 于点 E ，连接 BE 交 AC 于点 G ．试判断△ AED 和△ ABE 是否是“勤业三角形”？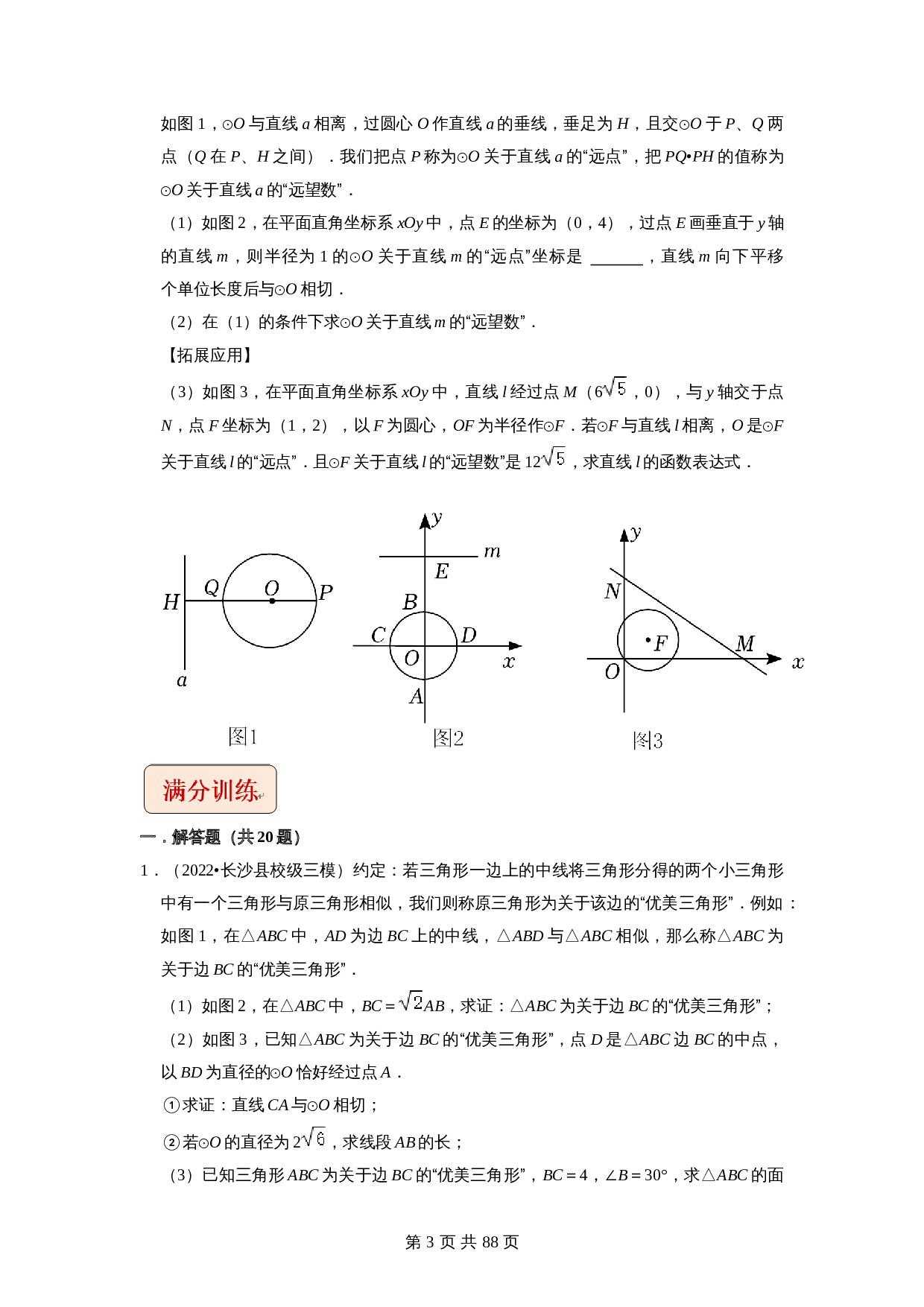如果是，请给出证明，并求出 的值；如果不是，请说明理由； （3）如图2，在（2）的条件下，当 AF ： FG ＝2：3时，求∠ BED 的余弦值． 【 例4】 （2022•清苑区二模）【问题提出】 如图1， ⊙ O 与直线 a 相离，过圆心 O 作直线 a 的垂线，垂足为 H ，且交 ⊙ O 于 P 、 Q 两点（ Q 在 P 、 H 之间）．我们把点 P