2024年中考数学压轴题之学霸秘笈大揭秘(全国通用)
专题31三角形与新定义综合问题
【
例1】
(2022•淮安区模拟)我们定义:等腰三角形中底边与腰的比叫做底角的邻对(
can
),如图1,在△
ABC
中,
AB
=
AC
,底角∠
B
的邻对记作
canB
,这时
canB
=
=
.容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题:
(1)
can
30°=
,若
canB
=1,则∠
B
=
°.
(2)如图2,在△
ABC
中,
AB
=
AC
,
canB
=
,
S
△
ABC
=48,求△
ABC
的周长.
【
例2】
(2022•柯城区校级三模)定义:若三角形的一条边上的高线与这条边相等,则称这个三角形为“标准三角形”.如:在△
ABC
,
CD
⊥
AB
于点
D
,
AB
=
CD
,则△
ABC
为标准三角形.
【概念感知】
判断:对的打“√”,错的打“×”.
(1)等腰直角三角形是标准三角形.
(2)顶角为30°的等腰三角形是标准三角形.
【概念理解】
若一个等腰三角形为标准三角形,则此三角形的三边长之比为
.
【概念应用】
(1)如图,若△
ABC
为标准三角形,
CD
⊥
AB
于点
D
,
AB
=
CD
=1,求
CA
+
CB
的最小值.
(2)若一个标准三角形的其中一边是另一边的
倍,求最小角的正弦值.
【
例3】
(2020•五华区校级三模)爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,
AM
、
BN
是
ABC
的中线,
AM
⊥
BN
于点
P
,像
ABC
这样的三角形均为“中垂三角形”.设
BC
=
a
,
AC
=
b
,
AB
=
c
.
【特例探究】
(1)如图1,当∠
PAB
=45°,
c
=
时,
a
=
,
b
=
;如图2,当∠
PAB
=30°,
c
=2时,
a
2
+
b
2
=
;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想
a
2
、
b
2
、
c
2
三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,在
▱
ABCD
中,
E
、
F
分别是
AD
、
BC
的三等分点,且
AD
=3
AE
,
BC
=3
BF
,连接
AF
、
BE
、
CE
,且
BE
⊥
CE
于
E
,
AF
与
BE
相交点
G
,
AD
=3
,
AB
=3,求
AF
的长.
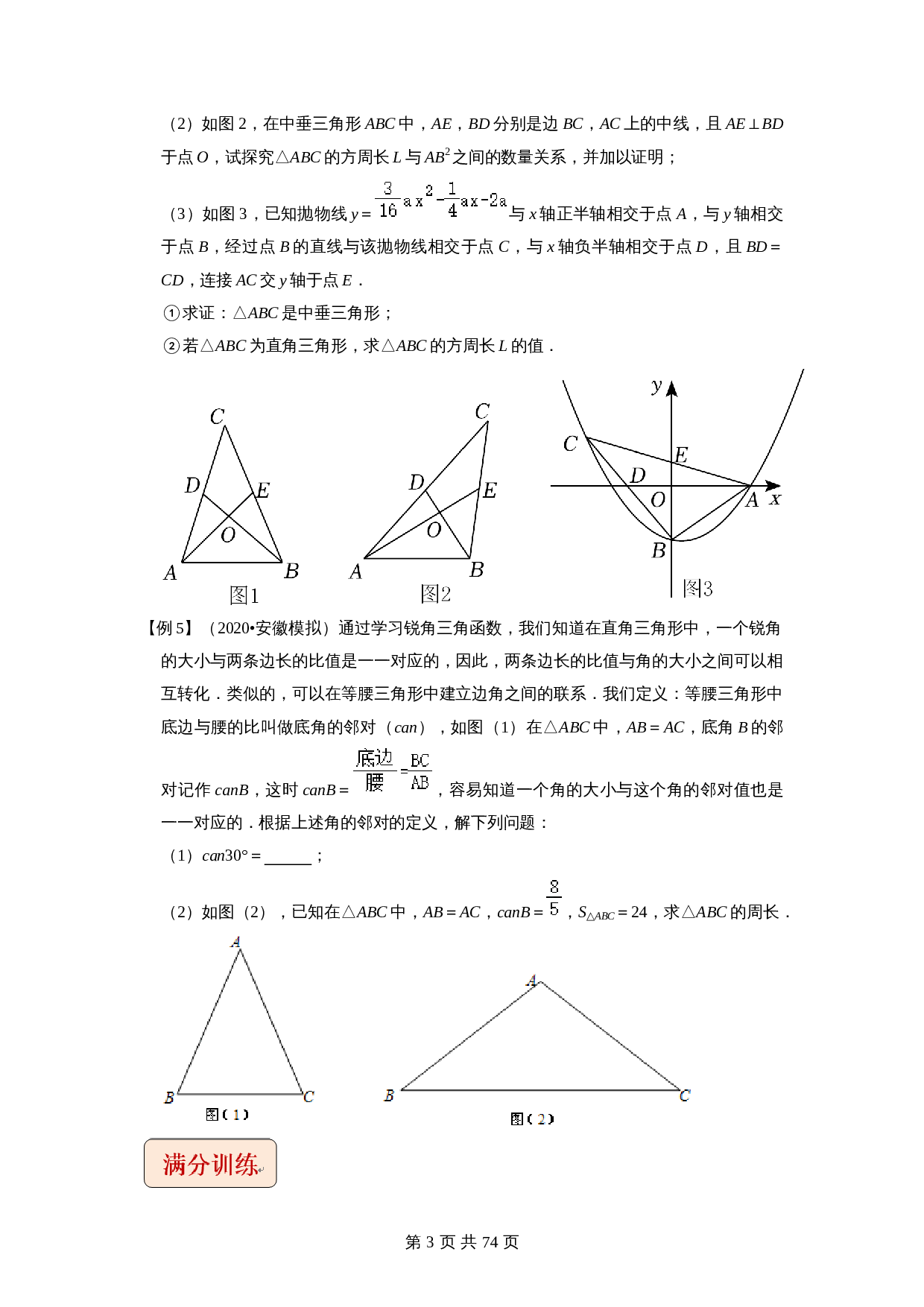
【
例4】
(2020•岳麓区校级二模)定义:在△
ABC
中,若有两条中线互相垂直,则称△
ABC
为中垂三角形,并且把
AB
2
+
BC
2
+
CA
2
叫做△
ABC
的方周长,记作
L
,即
L
=
AB
2
+
BC
2
+
CA
2
.
(1)如图1,已知△
ABC
是中垂三角形
【压轴题】专题31三角形与新定义综合问题(全国通用)(含解析)-2024年中考数学复习