【达标突破】苏科版九年级下册数学 第6章 图形的相似 单元测试（A卷·基础达标）（含解析）

第6章 图形的相似（ A卷·基础达标 ） 一、单选题 （本大题共 1 0 小题， 每小题3分， 共 3 0 分） 1．已知 ，则 ＝（      ） A． B． C． D． 2．如图，在 中， ， ，若 ，则 （     ） A． B． C． D． 3．如图，在直角坐标系中，△ OAB 的顶点为 O （0，0）， A （4，3）， B （3，0）．以点 O 为位似中心，在第三象限内作与△ OAB 的位似比为 的位似图形△ OCD ，则点 C 坐标（　　） A．（﹣1，﹣1） B．（﹣ ，﹣1） C．（﹣1，﹣ ） D．（﹣2，﹣1） 4．如图，在 中，点 分别在 边上， 与 不平行，那么下列条件中，不能判定 的是（      ） A． B． C． D． 5． 的三边长分别为2，3，4，另有一个与它相似的三角形 ，其最长边为12，则 的周长是（      ） A．54 B．36 C．27 D．21 6．如图，在 ABC 中， D 、 E 分别为线段 BC 、 BA 的中点，设 ABC 的面积为 S ， EBD 的面积为 S ．则 =（      ） A． B． C． D． 7．如图，某零件的外径为10cm，用一个交叉卡钳（两条尺长 AC 和 BD 相等）可测量零件的内孔直径 AB ．如果 OA ： OC = OB ： OD =3，且量得 CD =3cm，则零件的厚度 x 为（      ） A． B． C． D． 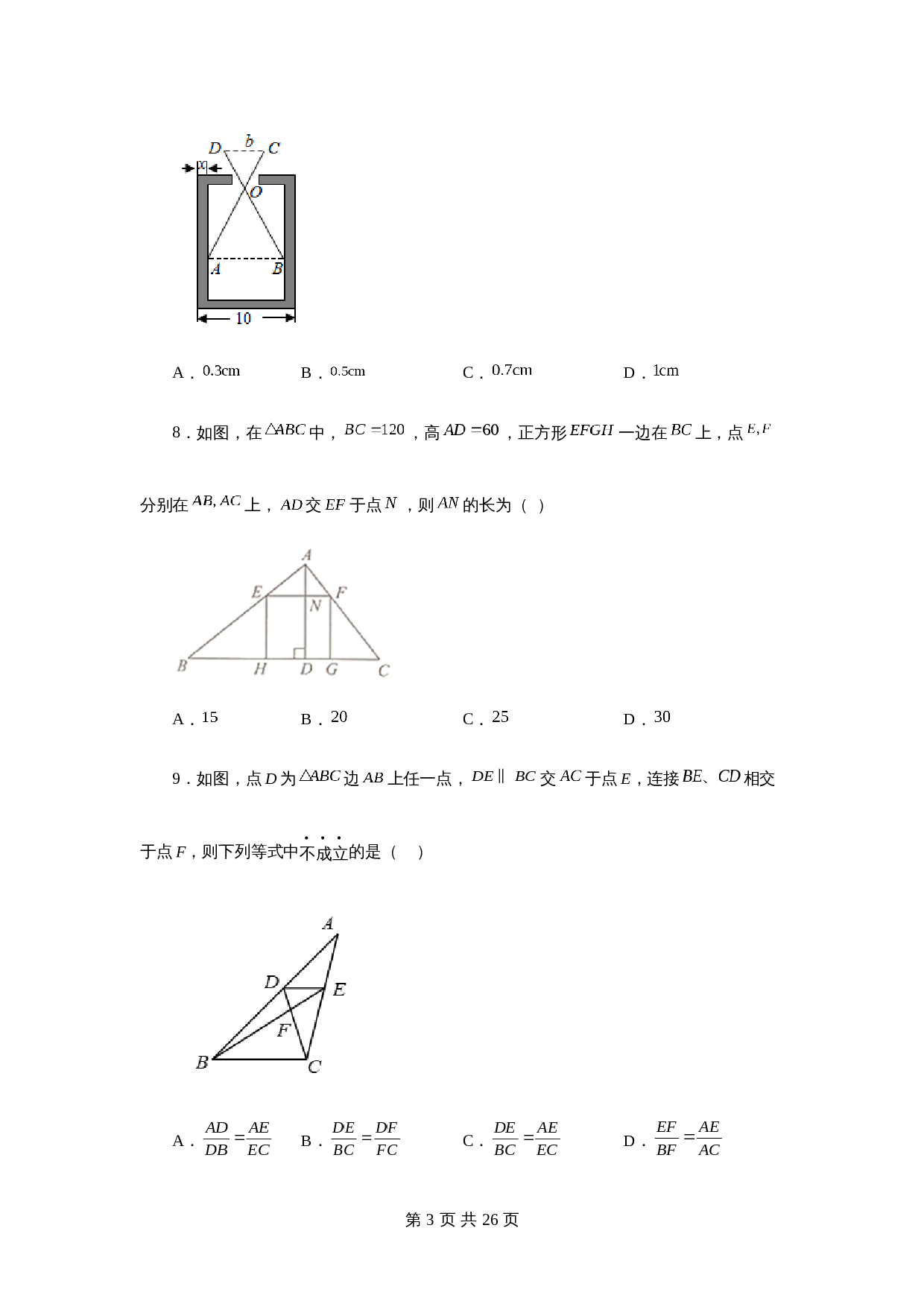8．如图，在 中， ，高 ，正方形 一边在 上，点 分别在 上， 交 于点 ，则 的长为（    ） A． B． C． D． 9．如图，点 D 为 边 上任一点， 交 于点 E ，连接 相交于点 F ，则下列等式中 不成立 的是（      ） A． B． C． D． 10．如图，点 ，将线段 平移得到线段 ，若 ，则点 D 的坐标是（      ） A． B． C． D． 二、填空题 （本大题共 8 小题， 每小题4分， 共 32 分） 11. 如图，直线 l 1 ∥ l 2 ∥ l 3 ，分别交直线 m 、 n 于点 A 、 B 、 C 、 D 、 E 、 F ，若 AB ： BC ＝5：3， DE ＝15，则 EF 的长为___． 12．如图，圆中扇子对应的圆心角 （ ）与剩余圆心角 的比值为黄金比时，扇子会显得更加美观，若黄金比取0.6，则 的度数是__________． 13．如图，在 中， ，点 是边 上的一点， 于 ，则边 的长为_____． 14．如图，在 中， ，过点 B 作 ，垂足为 B ，且 ，连接 CD ，与 AB 相交于点 M ，过点 M 作 ，垂足为 N ．若 ，则 MN 的长为__________． 15．《墨子·天文志》记载：“执规矩，以度天下之方圆．”度方知圆，感悟数学之美．如图，正方形 的面积为4，以它的对角线的交点为位似中心，作它的位似图形 ，若 ，则四边形 的外接圆的周长为___________． 16．如图，在△ ABC 中， D 在 AC 边上， AD ： DC ＝1：2， O 是 BD 的中点，连接 AO 并延长交 BC 于 E ，则 BE ： EC ＝___． 17．如图，矩形 ABCD 中， AB ＝2， BC ＝ ， E 为 CD 的中点，连接 AE 、 BD 交于点 P ，过点 P 作 PQ ⊥ BC 于点 Q ，则 PQ ＝_____． 18．如图，四边形 ABCD 中， AD ∥ BC ，对角线 AC ， BD 交于点 O ，已知 ，则 _________． 三、解答题 （本大题共 6 小题，共 58 分） 19． （8分） 如图，在 △ ABC中，BD、CE分别是AC、AB上的中线，BD与CE相交于点O． （1）利用尺规作图取线段CO的中点．（保留作图痕迹，不写作法）； （2）猜想CO与OE的长度有什么关系，并说明理由． 20． （8分） 如图，点 D 是△ ABC 的边 AB 上一点，∠ ABC ＝∠ ACD ． 求证：△ ABC ∽△ ACD ； 当 AD ＝2， AB ＝3时，求 AC 的长． 21． （10分） 如图，在平行四边形ABCD中，BC=8，点E、F是对角线BD上的两点，且BE=EF=FD，AE的延长线交BC于点G，GF的延长线交AD于点H． （1）求HD的长； （2）设 的面积为a，求四边形AEFH的面积．（用含a的代数式表示） 22． （10分） 如图，利用标杆 测量楼高，点 A ， D ， B 在同一直线上， ， ，垂足分别为 E ， C ．若测得 ， ， ，楼高 是多少？ 23． （10分） 如图， AC 是⊙ O 的直径，弦 BD 交 AC 于点 E ，点 F 为 BD 延长线上一点，∠ DAF ＝∠ B ． 求证： AF 是⊙ O 的切线； 若⊙ O 的半径为5， AD 是 AEF 的中线，且 AD ＝6，求 AE 的长． 24． （12分） 如图，折叠矩形OABC的一边BC，使点C落在OA边的点D处，已知折痕BE=5 ，且 ，以O为原点，OA所在的直线为x轴建立如图所示的平面直角坐标系，抛物线l：y=－ +c经过点E，且与AB边相交于点F． （1）求证：△ABD∽△ODE； （2）若M是BE的中点，连接MF，求证：MF⊥BD； （3）P是线段BC上一点，点Q在抛物线l上，且始终满足PD⊥DQ，在点P运动过程中，能否使得PD=DQ？若能，求出所有符合条件的Q点坐标；若不能，请说明理由． 参考答案 1．D 【分析】由题意易得 ，进而问题可求解． 解： 由 可得： ， ∴ ； 故选D． 【点拨】 本题主要考查比例的基本性质，熟练掌握比例的基本性质是解题的关键． 2．C 【分析】由 ， ，可得 再建立方程即可． 解： ， ， ， 解得： 经检验符合题意 故选C 【点拨】 本题考查的是平行线分线段成比例，证明“ ”是解本题的关键． 3．B 【分析】根据关于以原点为位似中心的对应点的坐标的关系，把 A 点的横纵坐标都乘以 即可． 解： ∵以点 O 为位似中心，位似比为 ， 而 A （4，3）， ∴ A 点的对应点