北师大版九,年级数学下册单元检测第1章-直角三角
形的边角关系(5)附答案
(满分:120分时限:100分钟)
一、认真填一填!请把你认为正确的结论填在题中的横线上。(每题3分,满分24分)
1.等腰直角三角形的一个锐角的余弦值等于
2.在△ABC中,LC=90°, sinA=
, cosA
3.比较下列三角函数值的大小:sin40°
cos400
2
4、化简:
5.若是锐角,cosA>
,则ZA应满足
6.小芳为了测量旗杆高度,在距棋杆底部6米处测得顶端的仰角是60°,已知小芳的身高
是1米5,则旗杆高
_米。 (保留1位小数)
7、某科技小组制作了一个机器人,它能根据指令要求进行行走和旋转.某一指令规定:
机器人先向正前方行走1米,然后左转45°.若机器人反复执行这一指令,则从出发到第
一次回到原处,机器人共走了
米.
8、已知菱形ABCD的边长为6,LA=60°,如果点P是菱形内一点,且PB=PD=
,那么AP的长为
二、你一定能选对!请把下列各题中惟一正确答案的代号填在题后的括号内(每题3分,
满分30分)
9、在Rt△ABC中,LC=90°,AC=3,BC=4,那么cosB的长是(
B.
D.
A.
C.
10、已知等边△ABC的边长为2,则其面积为
)
A.2
B.Z
c.2
D.4
11.在
中 C=90°,2A=B,LA:B:C对边分别为a、b、,则 a: b : c
等于(
)
A
B.
c.7
D.Z
12、在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值(
第1页共6页
A.扩大2倍
B.缩小2倍
C.扩大4倍
D.没有变化
13、某人沿着倾斜角α为的斜坡前进了100米,则他上升的最大高度是(
A.2
米
B.100sinα米
2
米
D.100cosα米
,则顶角为
(
)
A 600
B
900
C
1200
D
1500
15、如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在
CB的延长线上的D'处,那么tanBAD'等于(
B.Z
A.1
D.Z
A
D
B
(第15题图)
(第16题图)
(第17题图)
(第18题图)
16、如图,CD是平面镜,光线从A出发经CD上点E发射后照射到B点。若入射角为
α,ACCD,BDCD,垂足分别为C、D,且AC=3,BD=6,CD=11则tanα的
值为(
A.
B.
c.Z
D.D
17、如图,在300m高的峭壁上测得一塔的塔顶与塔基的俯角分别为30°和60°,则塔高
CD为(
)
A.200m
B.180m
C.150m
D.100m
18、如图,在矩形ABCD中,CEIBD于点E,BE=2,DE=8,则tanACE的值为(
)
A.P
B.2
c.2
D.2
四、解答题:(共66分)
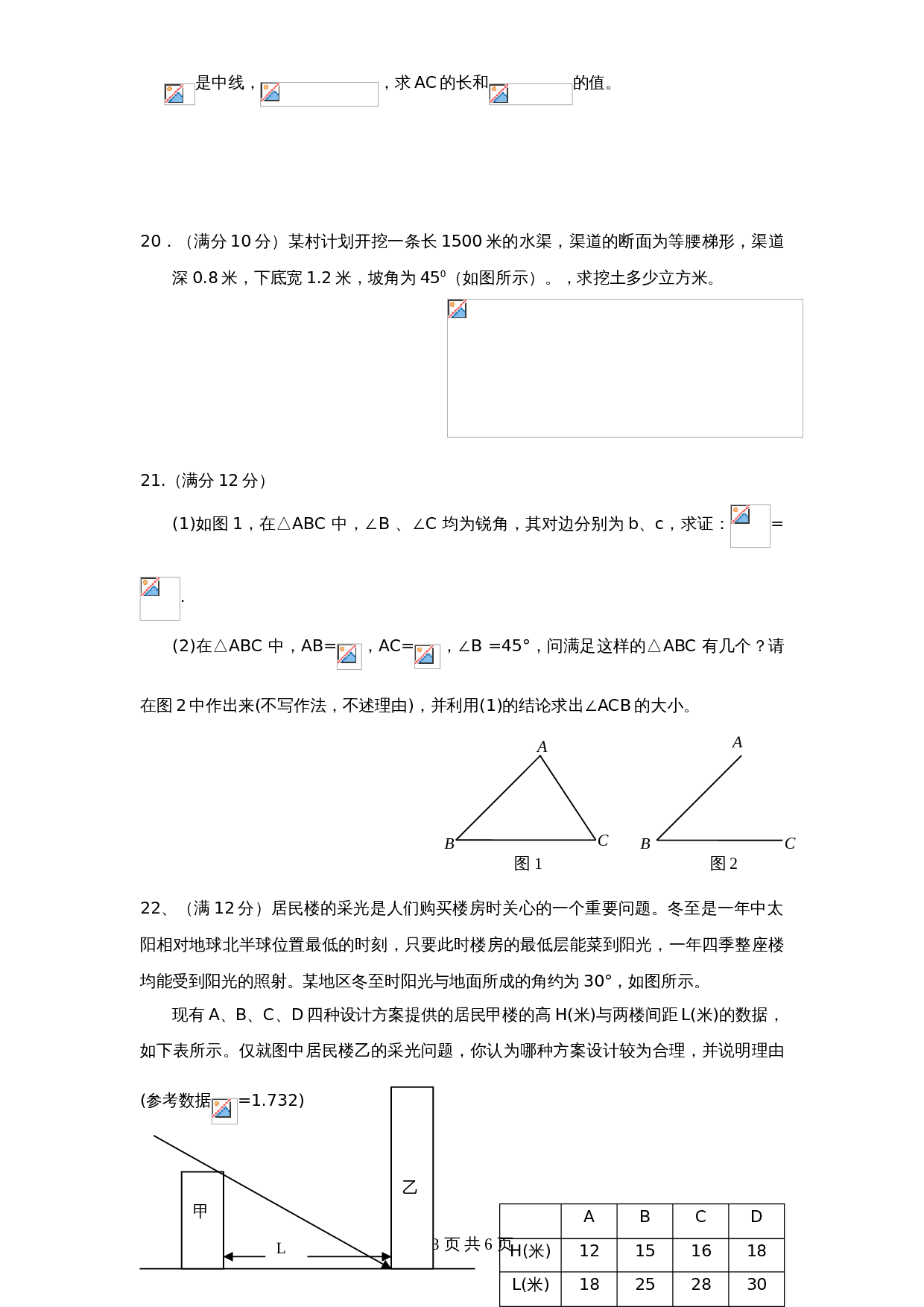
19.(满分10分)如图,在
中,国
第2页共6页
,求AC的长和
的值。
20.(满分10分)某村计划开挖一条长1500米的水渠,渠道的断面为等腰梯形,渠道
深0.8米,下底宽1.2米,坡角为45°(如图所示)。,求挖土多少立方米。
2
21. (满分12分)
(1)如图1,在△ABC中,ZB、ZC均为锐角,其对边分别为b、c,求证:
(2)在△ABC 中,AB=
B=45°,问满足这样的△ABC有几个?请
在图2中作出来(不写作法,不述理由),并利用(1)的结论求出乙ACB的大小。
A
C
图 1
图 2
22、(满12分)居民楼的采光是人们购买楼房时关心的一个重要问题。冬至是一年中太
阳相对地球北半球位置最低的时刻,只要此时楼房的最低层能菜到阳光,一年四季整座楼
均能受到阳光的照射。某地区冬至时阳光与地面所成的角约为30°,如图所示,
现有A、B、C、D四种设计方案提供的居民甲楼的高H(米)与两楼间距L(米)的数据
如下表所示。仅就图中居民楼乙的采光问题,你认为哪种方案设计较为合理,并说明理由
(参考数据=1.732)
Z
.
A
B
C
D
β页共6 H(米)
12
15
16
18
L(米)
18
25
28
30
北师大版九年级数学下册单元测试 第1章-直角三角形边角关系5(含答案)