【达标突破】苏科版九年级下册数学 第5章 二次函数 单元测试（C卷·拓展突破）（含解析）

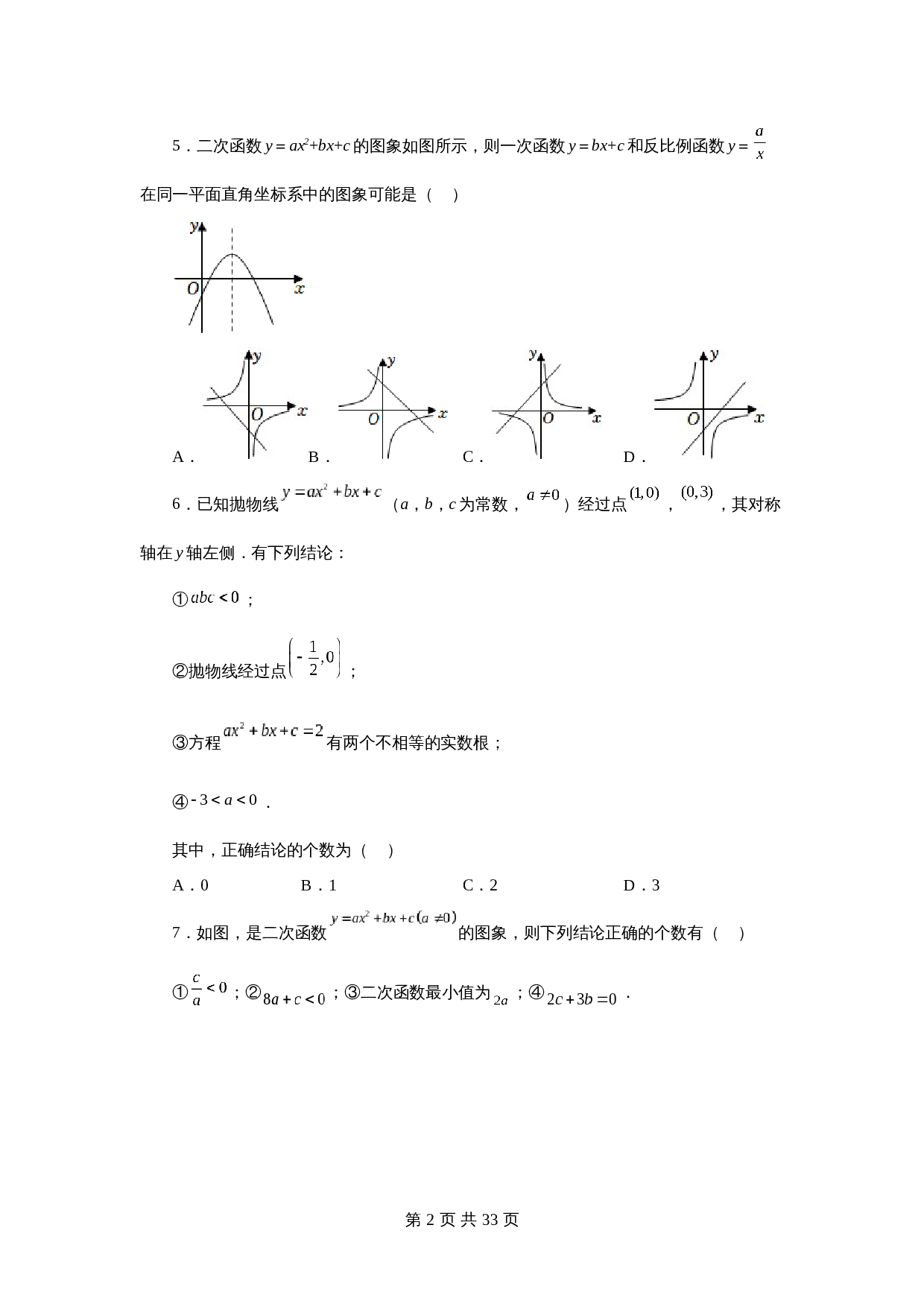
第5章 二次函数（ C卷·拓展突破 ） 单选题 （本大题共 1 0 小题， 每小题3分， 共 3 0 分） 1．下列函数：① ，② ，③ ，④ ， 是 的反比例函数的个数有（      ） A． 个 B． 个 C． 个 D． 个 2．对于抛物线 ，下列说法正确的是（　　） A．抛物线开口向上 B．当 时， y 随 x 增大而减小 C．函数最小值为﹣2 D．顶点坐标为（1，﹣2） 3．二次函数 的图象如图所示，若 在该函数的图象上，则 的大小关系是（     ） A． B． C． D． 4．在平面直角坐标系内，已知点 A （﹣1，0），点 B （1，1）都在直线 y ＝ 上，若抛物线 y ＝ ax 2 ﹣ x +1（ a ≠0）与线段 AB 有两个不同的交点，则 a 的取值范围是（　　） A． a ≤﹣2成 a ≥1 B． 或﹣2≤ a ≤1 C．1≤ 或 a ≤﹣2 D．﹣2≤ 5．二次函数 y ＝ ax 2 + bx + c 的图象如图所示，则一次函数 y ＝ bx + c 和反比例函数 y ＝ 在同一平面直角坐标系中的图象可能是（      ） A． B． C． D． 6．已知抛物线 （ a ， b ， c 为常数， ）经过点 ， ，其对称轴在 y 轴左侧．有下列结论： ① ； ②抛物线经过点 ； ③方程 有两个不相等的实数根； ④ ． 其中，正确结论的个数为（      ） A．0 B．1 C．2 D．3 7．如图，是二次函数 的图象，则下列结论正确的个数有（      ） ① ；② ；③二次函数最小值为 ；④ ． A．1个 B．2个 C．3个 D．4个 8．已知二次函数 ，当 时， 的最小值为 ，则 的值为（      ） A． 或4 B． 或 C． 或4 D． 或4 9．如图， 的三个顶点 A 、 C 、 D 都在二次函数 的图象上，斜边 平行于 x 轴，若斜边 上的高 长为 h ，则（      ） A． B． C． D． 10．函数 的图象是由函数 的图象 轴上方部分不变，下方部分沿 轴向上翻折而成，如图所示，则下列结论正确的是（      ） ① ；② ；      ③ ；④将图象向上平移1个单位后与直线 有3个交点． A．①② B．①③ C．②③④ D．①③④ 填空题 （本大题共 8 小题， 每小题4分， 共 32 分） 11．若 y ＝（ m +1） x 2 + mx ﹣1是关于 x 的二次函数，则 m 满足_____． 12．已知二次函数 ，当 时，函数值 y 的最小值为1，则 a 的值为_______． 13．抛物线 y = ax 2 + bx + c （ a ， b ， c 为常数）的部分图象如图所示，设 m = a - b + c ，则 m 的取值范围是______． 14．抛物线 上部分点的横坐标 ，纵坐标 的对应值如下表： … －2 －1 0 1 2 … … 0 4 6 6 4 … 请求出当 ＜0时 的取值范围 ________． 15．如图，抛物线 与 x 轴交于 A 、 B 两点，且点 A 、 B 都在原点右侧，抛物线的顶点为点 P ，当 为直角三角形时， m 的值为________． 16．如图，已知顶点为（﹣3，﹣6）的抛物线 y ＝ ax 2 ＋ bx ＋ c 过点（﹣1，﹣4），则下列结论：①对于任意的 x ＝ m ，均有 am 2 ＋ bm ＋ c ≥﹣6；② ac ＞0；③若点（ ），（ ， y 2 ）在抛物线上，则 y 1 ＞ y 2 ；④关于 x 的一元二次方程 ax 2 ＋ bx ＋ c ＝﹣4的两根为﹣5和﹣1；⑤ b ﹣6 a ＝0；其中正确的有_______（填序号）． 17．如图，已知函数 与 的图象交于点 ，点 的纵坐标为1，则关于 的方程 的解为_____________． 18．如图，在平面直角坐标系中，抛物线 y = x 2 + mx 交 x 轴的负半轴于点 A ．点 B 是 y 轴正半轴上一点，点 A 关于点 B 的对称点 A ′恰好落在抛物线上．过点 A ′作 x 轴的平行线交抛物线于另一点 C ．若点 A ′的横坐标为1，则 A ′ C 的长为_____． 三、解答题 （本大题共 6 小题，共 58 分） 19． （8分） 如图，直线 l 过 x 轴上一点 ，且与抛物线 相交于 B 、 C 两点． B 点坐标为 ． (1) 求抛物线解析式； (2) 若抛物线上有一点 D （在第一象限内），使得 ，求点 D 的坐标． 20． （8分） 已知二次函数 ． (1) 用配方法把这个二次函数化成 的形式； (2) 在所给的平面直角坐标系中，画出这个二次函数的图象； (3) 当 时，结合图象直接写出 y 的取值范围． 21． （10分） 某文具连锁店专售一款钢笔，每支钢笔的成本为20元/支，销售中发现，该钢笔每天的销售量 y （支）与销售单价 x （元/支）之间存在如图所示的关系，由于武汉疫情的爆发，该文具连锁店店主决定从每天获得的利润中抽出200元捐献给武汉． (1) 求 y 与 x 之间的函数关系式． (2) 当销售单价为多少元时，文具店获利最大？最大利润是多少？ (3) 为了保证捐款后每天剩余利润为550元，这款钢笔的销售单价是多少？ 22． （10分） 如图，二次函数 与 x 轴交于 A ， B 两点，与 y 轴交于 C 点．已知，点 A 的坐标为（–1，0）． (1) 求这个二次函数图象的顶点坐标； (2) 已知第一象限内的点 D （ m ， m ＋1）在二次函数图象上，探究 CD 与 x 轴的位置关系； (3) 在（2）的条件下，求点 D 关于直线 BC 的对称点 的坐标． 23． （10分） 已知抛物线经过 A （－1，0）、 B （0、3）、 C （3，0）三点， O 为坐标原点，抛物线交正方形 OBDC 的边 BD 于点 E ，点 M 为射线 BD 上一动点，连接 OM ，交 BC 于点 F (1) 求抛物线的表达式； (2) 求证：∠ BOF ＝∠ B